논문 링크 : https://arxiv.org/abs/1710.10903
1. Introduction
On the other hand, we have non-spectral approaches (Duvenaud et al., 2015; Atwood & Towsley, 2016; Hamilton et al., 2017), which define convolutions directly on the graph, operating on groups of spatially close neighbors.
One of the benefits of attention mechanisms is that they allow for dealing with variable sized inputs, focusing on the most relevant parts of the input to make decisions.
When an attention mechanism is used to compute a representation of a single sequence, it is commonly referred to as self-attention or intra-attention.
Inspired by this recent work, we introduce an attention-based architecture to perform node classification of graph-structured data. The idea is to compute the hidden representations of each node in the graph, by attending over its neighbors, following a self-attention strategy. The attention architecture has several interesting properties: (1) the operation is efficient, since it is parallelizable across node-neighbor pairs; (2) it can be applied to graph nodes having different degrees by specifying arbitrary weights to the neighbors; and (3) the model is directly applicable to inductive learning problems, including tasks where the model has to generalize to completely unseen graphs. We validate the proposed approach on four challenging benchmarks: Cora, Citeseer and Pubmed citation networks as well as an inductive protein-protein interaction dataset, achieving or matching state-of-the-art results that highlight the potential of attention-based models when dealing with arbitrarily structured graphs.
- graph-structured data에서 node classification을 수행하기 위해 attention-based 구조를 소개할 것이다. 이 아이디어는 self-attention 전략에 따라 neighbor에 관심을 두어 각 node의 hidden representation을 계산하는 것이다.
- 이 attention architecture은 몇 가지 흥미로운 특성들이 있다.
- node-neighbor pairs를 병렬화할 수 있으므로 계산이 효율적이다.
- neighbor에 임의의 가중치를 지정하여 degree가 다른 그래프 node에도 적용할 수 있다.
- 이 모델은 모델이 완전히 본 적이 없는 그래프를 generalize 해야하는 작업을 포함하여 inductive한 학습 문제에 직접적으로 적용가능하다
- 4가지 데이터셋 사용 : (Citation network)Citeseer, Cora, Pubmed / protein-protein interaction dataset
Moreover, our approach of sharing a neural network computation across edges is reminiscent of the formulation of relational networks and VAIN, wherein relations between objects or agents are aggregated pair-wise, by employing a shared mechanism.
- Edges에서 신경망 계산을 공유하는 접근방식은 공유 mechanism을 사용하여 객체와 agents 사이의 관계가 쌍으로 집계되는 관계형 네트워크 및 VAIN의 공식화를 연상시킨다.
Similarly, our proposed attention model can be connected to the works by Duan et al. (2017) and Denil et al. (2017), which use a neighborhood attention operation to compute attention coefficients between different objects in an environment.
- 여기서 제안한 attention model은 환경에서 서로 다른 객체 사이의 attention coefficients를 계산하기 위해 neighborhood attention operation을 사용한다.
다른 방법들 (locally linear embedding(LLE), memory networks)와의 비슷한 점 언급
2. GAT architecture
In this section, we will present the building block layer used to construct arbitrary graph attention networks (through stacking this layer), and directly outline its theoretical and practical benefits and limitations compared to prior work in the domain of neural graph processing.
2.1 Graph Attentional Layer
We will start by describing a single graph attentional layer, as the sole layer utilized throughout all of the GAT architectures used in our experiments
The particular attentional setup utilized by us closely follows the work of Bahdanau et al. (2015)—but the framework is agnostic to the particular choice of attention mechanism.
- agnostic은 'someone who does not know'와 같은 의미로 논문에서는 '물체의 종류를 모르는' 의미로 사용되는 것 같다.
- 여기서 사용하는 특정 attentional setup은 논문의 작업을 밀접하게 따르지만, framework는 attention mechanism에 대한 특정 선택에 대해 종류를 모른다. (이런식으로 해석 해야 할 것 같음.)
The input to our layer is a set of node features, , where N is the number of nodes, and F is the number of features in each node. The layer produces a new set of node features (of potentially different cardinality ), , as its output.
- input과 output의 형태. node features의 set 형태로 나옴. (input과 output은 cardinality, 즉 차원이 다를 수 있음.)
In order to obtain sufficient expressive power to transform the input features into higher-level features, at least one learnable linear transformation is required. To that end, as an initial step, a shared linear transformation, parametrized by a weight matrix, , is applied to every node. We then perform self-attention on the nodes—a shared attentional mechanism a : computes attention coefficients that indicate the importance of node j’s features to node i.
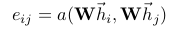
- shared linear transformation을 위해, weight matrix 가 모든 node에 적용된다. attentional mechanism이 attention coefficients를 계산하는데, 이는 j번째 node features기 i번째 node features에 미치는 중요성에 대해 말한다.
In its most general formulation, the model allows every node to attend on every other node, dropping all structural information. We inject the graph structure into the mechanism by performing masked attention—we only compute for nodes j ∈ , where is some neighborhood of node i in the graph.
- 가장 일반적인 공식에서, 모델이 모든 노드가 다른 노드에 연결되도록 허락하여 구조적 정보를 삭제한다. 논문에서는 masked attention을 수행하여 메커니즘에 graph structure를 삽입한다. 노드 N_i에 속해있는 j에 대해서만 e_ij를 계산하는데, 여기서 N_i는 i의 neighborhood이다.
In all our experiments, these will be exactly the first-order neighbors of i (including i). To make coefficients easily comparable across different nodes, we normalize them across all choices of j using the softmax function:
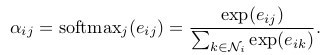
- 이 실험에서, 위의 내용은 정확하게 i의 first-order neighbors(i 포함)일 것이다. 이 coefficients들을 다른 노드들에 대해 비교하기 쉽게 만들기 위해 softmax function을 적용시킨다.
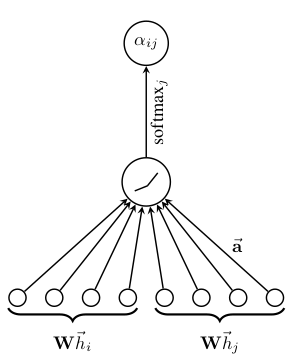
In our experiments, the attention mechanism a is a single-layer feedforward neural network, parametrized by a weight vector , and applying the LeakyReLU nonlinearity (with negative input slope α = 0.2). Fully expanded out, the coefficients computed by the attention mechanism (illustrated by Figure 1 (left)) may then be expressed as:
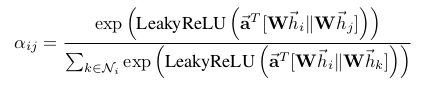
where · T represents transposition and || is the concatenation operation.
Once obtained, the normalized attention coefficients are used to compute a linear combination of the features corresponding to them, to serve as the final output features for every node (after potentially applying a nonlinearity, σ):
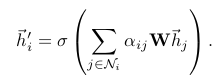
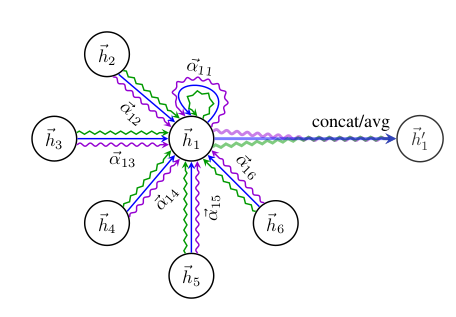
To stabilize the learning process of self-attention, we have found extending our mechanism to employ multi-head attention to be beneficial, similarly to Vaswani et al. (2017). Specifically, K independent attention mechanisms execute the transformation of Equation 4, and then their features are concatenated, resulting in the following output feature representation:
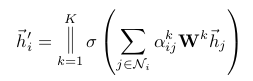
where || represents concatenation, are normalized attention coefficients computed by the k-th attention mechanism (), and is the corresponding input linear transformation’s weight matrix. Note that, in this setting, the final returned output, , will consist of features (rather than ) for each node.
- 위의 연산을 끝내고 나면 h' 는 cardinality가 F'이 아니고 KF'이 된다.
Specially, if we perform multi-head attention on the final (prediction) layer of the network, concatenation is no longer sensible—instead, we employ averaging, and delay applying the final nonlinearity (usually a softmax or logistic sigmoid for classification problems) until then:
- 만약 우리가 final layer에서 multi-head attention을 수행하고 싶다면, concatenation은 더 이상 sensible하지 않다. 대신에 우리는 averaging과 final nonlinearity를 나중으로 미룬다.
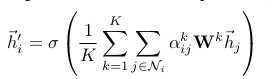
2.2 Comparisons to Related Work
The graph attentional layer described in subsection 2.1 directly addresses several issues that were present in prior approaches to modelling graph-structured data with neural networks:
- Computationally, it is highly efficient: the operation of the self-attentional layer can be parallelized across all edges, and the computation of output features can be parallelized across all nodes. No eigen-decompositions or similar costly matrix operations are required.
- As opposed to GCNs, our model allows for (implicitly) assigning different importances to nodes of a same neighborhood, enabling a leap in model capacity. Furthermore, analyzing the learned attentional weights may lead to benefits in interpretability, as was the case in the machine translation domain.
- The attention mechanism is applied in a shared manner to all edges in the graph, and therefore it does not depend on upfront access to the global graph structure or (features of) all of its nodes (a limitation of many prior techniques). This has several desirable implications:
- The graph is not required to be undirected (we may simply leave out computing if edge j → i is not present).
- It makes our technique directly applicable to inductive learning—including tasks where the model is evaluated on graphs that are completely unseen during training.
- The recently published inductive method of Hamilton et al. (2017) samples a fixed-size neighborhood of each node, in order to keep its computational footprint consistent; this does not allow it access to the entirety of the neighborhood while performing inference. This assumes the existence of a consistent sequential node ordering across neighborhoods, and the authors have rectified it by consistently feeding randomly-ordered sequences to the LSTM. Our technique does not suffer from either of these issues—it works with the entirety of the neighborhood (at the expense of a variable computational footprint, which is still on-par with methods like the GCN), and does not assume any ordering within it.
We were able to produce a version of the GAT layer that leverages sparse matrix operations, reducing the storage complexity to linear in the number of nodes and edges and enabling the execution of GAT models on larger graph datasets. However, the tensor manipulation framework we used only supports sparse matrix multiplication for rank-2 tensors, which limits the batching capabilities of the layer as it is currently implemented (especially for datasets with multiple graphs). Appropriately addressing this constraint is an important direction for future work.
3. Evaluation
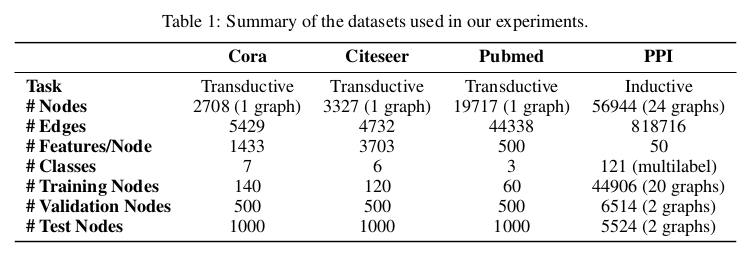
3.1 Datasets
Transductive learning
Cora, Citeseer, Pubmed
Inductive learning
PPI (protein-protein interaction)
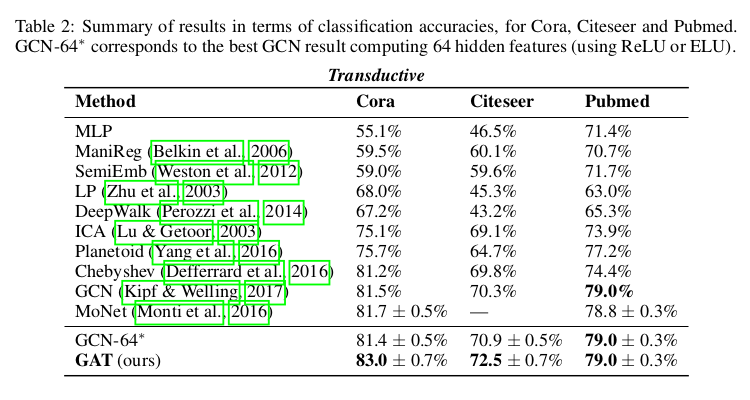
3.4 Results
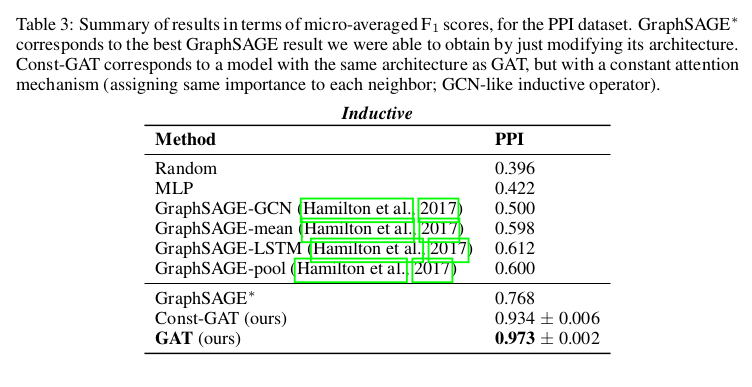

4. Conclusions
We have presented graph attention networks (GATs), novel convolution-style neural networks that operate on graph-structured data, leveraging masked self-attentional layers. The graph attentional layer utilized throughout these networks is computationally efficient (does not require costly matrix operations, and is parallelizable across all nodes in the graph), allows for (implicitly) assigning different importances to different nodes within a neighborhood while dealing with different sized neighborhoods, and does not depend on knowing the entire graph structure upfront—thus addressing many of the theoretical issues with previous spectral-based approaches.
- 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.
Uploaded by N2T
'Paper Summary' 카테고리의 다른 글
| Generative Adversarial Networks, NIPS’14 (0) | 2023.03.26 |
|---|---|
| DCGAN, ICLR’16 (0) | 2023.03.26 |
| GaAN: Gated Attention Networks for Learning on Large and Spatiotemporal Graphs, UAI’18 (0) | 2023.03.26 |
| Learning Actor Relation Graphs for Group Activity Recognition, CVPR’19 (0) | 2023.03.26 |
| Mesh Graphormer, ICCV’21 (0) | 2023.03.26 |