HOPE-Net: A Graph-based Model for Hand-Object Pose Estimation, CVPR’20

논문 링크 : https://openaccess.thecvf.com/content_CVPR_2020/papers/Doosti_HOPE-Net_A_Graph-Based_Model_for_Hand-Object_Pose_Estimation_CVPR_2020_paper.pdf

Abstract

Hand-Object pose estimation(HOPE)는 손과 들고 있는 물체의 포즈를 동시에 감지하는 것을 목표로 한다. 본 논문에서는 2D와 3D에서 실시간으로 손과 물체의 포즈를 추정하는 HOPE-Net이라는 lightweight model을 제안한다. 여기에서는 두 가지의 adaptive graph convolution 을 사용하는데, 하나는 hand joint와 object corner의 2D 좌표를, 하나는 2D 좌표를 3D 좌표로 변환하는 것이다.

1. Introduction

We model hand-object interaction by representing the hand and object as a single graph. Our model first predicts 2D keypoint locations of hand joints and object boundaries. Then the model jointly recovers the depth information from the 2D pose estimates in a hierarchical manner (Figure 1).

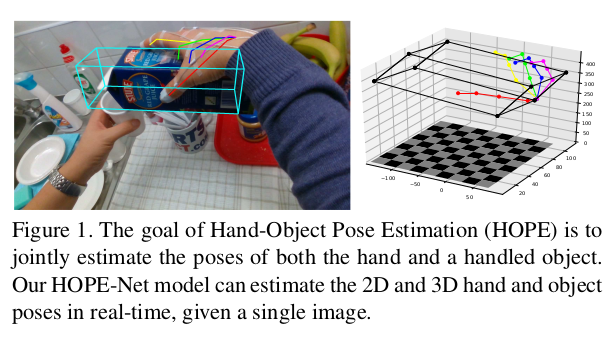
• 저자는 손과 물체를 하나의 그래프로 표현하여 hand-object interaction을 모델링한다. 모델은 먼저 hand joint와 object boundary의 2D keypoint location을 예측한다. 그런 다음 계층적 방식으로 2D pose 추정값에서 depth정보를 복구한다.

Our graph convolutional approach allows us to use a detection-based model to detect the hand keypoints in 2D (which is easier than predicting 3D coordinates), and then to accurately convert them to 3D coordinates. We show that using this graph-based network, we are not limited to training on only annotated real images, but can instead pre-train the 2D to 3D network separately with synthetic images rendered from 3D meshes of hands interacting with objects (e.g. ObMan dataset [10]). This is very useful for training a model for hand-object pose estimation as real-world annotated data for these scenarios is scarce and costly to collect.

• 그래프 컨볼루션 방식을 사용하면 detection-based model을 사용하여 2D에서 hand keypoint를 detect하고, 이를 3D 좌표로 정확하게 변환할 수 있는데, 이는 3D 좌표를 예측하는 것 보다 쉽다. 논문에서는 이 그래프 기반 네트워크를 사용하여 annotation이 된 real image에 학습하는 것 뿐만 아니라 object와 interaction하고있는 hand에대한 3D mesh로부터 렌더링된 synthetic image를 사용하여 2D to 3D network를 개별적으로 pre-train할 수 있음을 보인다. 이것은 annotation이 있는 데이터가 드물고 수집하는 데 비용이 많이 들기에 hand-object pose estimation을 위한 모델을 학습하는 데 매우 유용하다.

Contribution

We propose a novel but lightweight deep learning framework, HOPE-Net, which can predict 2D and 3D coordinates of hand and hand-manipulated object in real-time. Our model accurately predicts the hand and object pose from single RGB images.

• 손과 조작되고 있는 물체의 2D 및 3D 좌표를 실시간으로 예측할 수 있는 novel하고 가벼운 deep learning framework인 HOPE-Net 제안. 이는 single RGB image로부터 hand, object pose를 정확하게 예측한다.

We introduce the Adaptive Graph U-Net, a graph convolution-based neural network to convert 2D hand and object poses to 3D with novel graph convolution, pooling, and unpooling layers. The new formulations of these layers make it more stable and robust compared to the existing Graph U-Net [5] model.

• novel graph convolution, pooling, unpooling layer를 사용하여 2D hand와 object를 3D로 변환하는 Adaptive Graph U-Net 소개. 이러한 레이어의 새로운 공식은 기존 Graph U-Net 모델에 비해 더 안정적이고 견고하다.

Through extensive experiments, we show that our approach can outperform the state-of-the-art models for joint hand and object 3D pose estimation tasks while still running in real-time.

• 광범위한 실험을 통해 실시간으로 실행되는 동안 SOTA 모델보다 성능이 뛰어남을 보임.

3. Methodology

We now present HOPE-Net, which consists of a convolutional neural network for encoding the image and predicting the initial 2D locations of the hand and object key points (hand joints and tight object bounding box corners), a simple graph convolution to refine the predicted 2D predictions, and a Graph U-Net architecture to convert 2D keypoints to 3D using a series of graph convolutions, poolings, and unpoolings. Figure 2 shows an overall schematic of the HOPE-Net architecture.

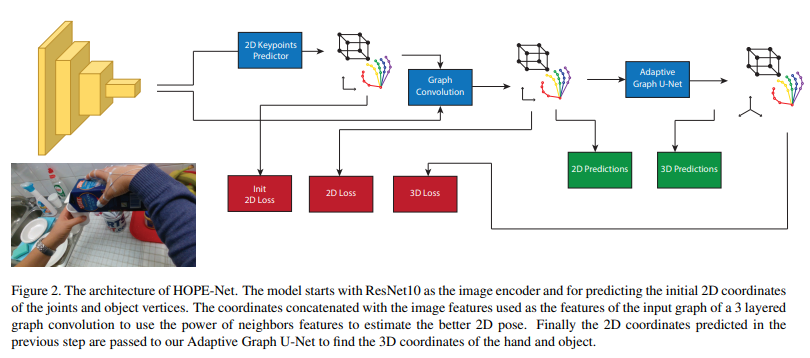
• HOPE-Net은 이미지를 인코딩하고 hand와 object key point(hand joint와 object bounding box corners)의 2D location을 예측하기위한 CNN, 예측된 2D prediction을 refine하기 위한 simple graph convolution, graph convolution, pooling, unpooling을 이용해 2D keypoint를 3D로 변환시키기 위한 Graph U-Net으로 구성되어 있다. 위는 HOPE-Net의 구조에 대한 모식도이다.

3.1. Image Encoder and Graph Convolution

For the image encoder, we use a lightweight residual neural network [11] (ResNet10) to help reduce overfitting. The image encoder produces a 2048D feature vector for each input image. Then initial predictions of the 2D coordinates of the keypoints (hand joints and corners of the object’s tight bounding box) are produced using a fully connected layer. We concatenate these features with the initial 2D predictions of each keypoint, yielding a graph with 2050 features (2048 image features plus initial estimates of x and y) for each node. A 3-layer adaptive graph convolution network is applied to this graph to use adjacency information and modify the 2D coordinates of the keypoints. The concatenation of the image features to the predicted x and y of each keypoint forces the graph convolution network to modify the 2D coordinates conditioned on the image features as well as the initial prediction of the 2D coordinates. These final 2D coordinates of the hand and object keypoints are then passed to our adaptive Graph U-Net, a graph convolution network using adaptive convolution, pooling, and unpooling to convert 2D coordinates to 3D.

• 이미지 인코더의 경우 overfitting을 줄이기 위해 lightweight model인 ResNet10을 사용한다. 이미지 인코더는 각 input 이미지에 대해 2048-D feature vector를 생성한다. 그런 다음 FC-layer를 사용하여 keypoint(hand joint, object tight bounding box에 대한 corner)의 2D 좌표인 initial prediction이 생성된다. 이 feature를 각 keypoint의 2D initial prediction과 concat하여 2050-D(2048 + 2D coordinate) node feature를 가지는 그래프를 생성한다. 이 그래프에 3-layer adaptive graph convolution network를 적용하여 인접 정보를 사용하고 keypoint 2D 좌표를 수정한다. 각 keypoint의 예측된 x, y와 image feature의 concat은 GCN이 2D 좌표의 초기 예측뿐만 아니라 이미지 feature에 대해 조절된 2D 좌표를 수정하도록 한다. hand, object keypoint의 최종 2D 좌표는 adaptive convolution, pooling 및 unpooling을 사용하여 2D 좌표를 3D로 변환하는 GCN인 Adaptive Graph U-Net으로 전달된다.

3.2. Adaptive Graph U-Net

We explain our graph-based model which predicts 3D coordinates of the hand joints and object corners based on predicted 2D coordinates. In this network, we simplify the input graph by applying graph pooling in the encoding part, and in the decoding part, we add those nodes again with our graph unpooling layers. Also, similar to the classic U-Net [23], we use skip connections and concatenate features from the encoding stage to features of the decoding stage in each decoding graph convolution. With this architecture we are interested in training a network which simplifies the graph to obtain global features of the hand and object, but also tries to preserve local features via the skip connections from the encoder to the decoder layers.

• 이번 섹션에서는 예측된 2D 좌표를 기반으로 hand joint와 object corners의 3D 좌표를 예측하는 graph-based model을 설명한다. 이 네트워크에서는 인코딩 부분에서 graph pooling을 적용하여 input graph를 단순화하고 디코딩 부분에서 unpooling layer를 사용하여 해당 노드를 다시 추가한다. 또한, 기존의 U-Net과 유사하고 각 decoding graph convolution에서 skip connection을 사용하고 인코딩 단계의 feature를 decoding 단계의 feature로 연결한다. 이 아키텍처를 통해 저자는 손과 물체의 global feature를 얻기위해 그래프를 단순화하는 네트워크의 학습뿐만아니라 encoder로부터 decoder계층으로의 skip connection을 통해 local feature를 보존하기위해 시도한다.

We found that the sigmoid function in the pooling layer of [5] (gPool) can cause the gradients to vanish and to not update the picked nodes at all. We thus use a fully-connected layer to pool the nodes and updated our adjacency matrix in the graph convolution layers, using the adjacency matrix as a kernel we apply to our graph. In graphs with sparse adjacency matrices, such as when the graph is a mesh or a hand or body skeleton, removing one node and its edges may cut the graph into several isolated subgraphs and destroy the connectivity, which is the most important feature of a graph convolutional neural network. Using an adaptive graph convolution neural network, we avoid this problem as the network finds the connectivity of the nodes after each pooling layer.

• 저자는 [5](gPool)의 pooling layer에 있는 sigmoid 함수가 gradient vanishing 문제가 있고, 선택한 node를 전혀 업데이트하지 않을 수 있음을 발견하였다. 따라서, FC-layer를 사용하여 노드를 풀링하고 adjacency matrix를 그래프에 적용하는 kernel로 사용하여 graph convolution layer에서 adjacency matrix를 업데이트 하였다. 그래프가 mesh, hand or body skeleton인 경우와 같이 sparse adjacency matrix인 경우, 하나의 노드와 해당되는 edge를 제거하면 그래프가 여러 개의 subgraph로 절단되는데 이는 GCN에서의 가장 중요한 기능인 connectivity가 손상될 수 있다. 이러한 문제를 방지하기 위해 Adaptive graph convolution을 사용하는데 이는 각 pooling layer 이후에 node의 연결성을 찾는다.

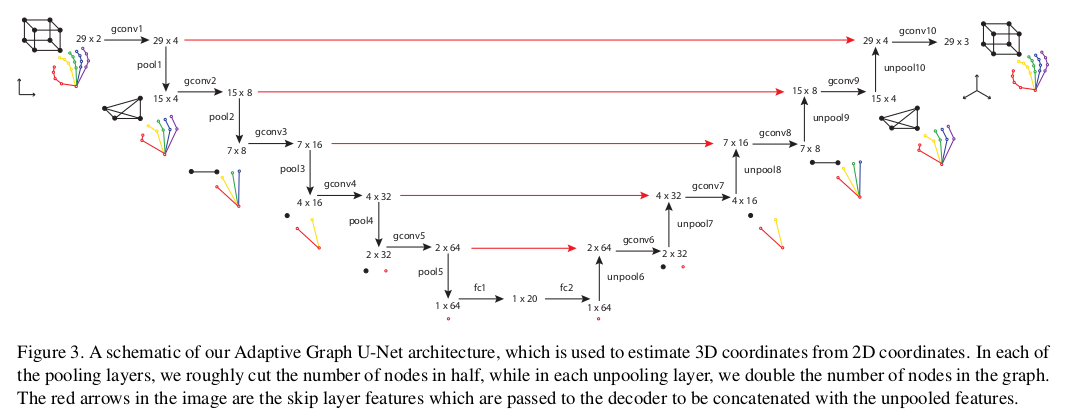
• 2D coordinate로부터 3D coordinate를 estimate하는 network인 Adaptive Graph U-Net architecture이다. pooling layer를 통해 대략 절반의 node를 cut하고, unpooling layer를 통해 graph node를 2배로 늘린다. 빨간색 선은 skip layer feature이다.

3.2.1. Graph Convolution

• 이는 이전 GCN 논문과 같은 연산을 실행한다.

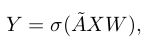
• 여기서 function은 activation function(본 논문에서는 ReLU 사용), W는 trainable weight matrix, X는 input feature, $\tilde{A}$ 는 renormalization trick을 적용한 adjacency matrix이다.

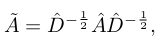
So ÃX is the new feature matrix in which each node’s features are the averaged features of the node itself and its adjacent nodes. Therefore, to effectively formulate the HOPE problem in this framework, an effective adjacency matrix is needed.

• 따라서 ÃX는 각 노드의 feature가 해당 노드와 인접 노드의 averaged feature인 새로운 feature matrix이다. 따라서, 이 프레임워크에서 HOPE problem을 효과적으로 공식화하기 위해서는 효과적인 인접행렬이 필요로한다.

Initially, we tried using the adjacency matrix defined by the kinematic structure of the hand skeleton and the object bounding box for the first layer of the network. But we found it was better to allow the network to learn the best adjacency matrix. Note that this is no longer strictly an adjacency matrix in the strict sense, but more like an “affinity” matrix where nodes can be connected by weighted edges to many other nodes in the graph. An adaptive graph convolution operation updates the adjacency matrix (A), as well as the weights matrix (W ) during the back-propagation step. This approach allows us to model subtle relationships between joints which are not connected in the hand skeleton model (e.g. strong relationships between finger tips despite not being physically connected).

• 처음에 저자는 hand skeleton의 kinematic structure와 object bounding box에 의해 정의된 adjacency matrix를 사용하려 했다. 그러나, 네트워크가 최상의 adjacency matrix를 학습하도록 하는 것이 다 낫다는 것을 발견했다. 이는 더 이상 엄밀한 의미의 adjacency matrix가 아니라 그래프의 다른 노드에 가중치를 적용하여 노드를 연결할 수 있는 “친화도” 행렬에 더 가깝다. Adaptive graph convolution 연산은 adjacency matrix (A), weight matrix (W)를 back-propagation step 동안 업데이트한다. 이 접근 방식을 사용하면 hand skeleton model에서 연결되지 않은 joint간의 관계를 모델링할 수 있다. (예: 물리적으로 연결되지 않았음에도 불구하고 finger tip 사이의 강한 관계)

3.2.2 Graph Pooling

As mentioned earlier, we did not find gPool [5] helpful in our problem: the sigmoid function’s weaknesses are well-known [16, 18] and the use of sigmoid in the pooling step created very small gradients during backpropagation. This caused the network not to update the randomly-initialized selected pooled nodes throughout the entire training phase, and lost the advantage of the trainable pooling layer. To solve this problem, we use a fully-connected layer and apply it on the transpose of the feature matrix. This fully-connected works as a kernel along each of the features and outputs the desired number of nodes. Also due to using an adaptive graph convolution, this pooling does not fragment the graph into pieces.

• 앞에 언급했듯이 gPool 이 이 문제에 도움이 되지 않는다는 것을 발견했다: sigmoid를 사용하면 역전파 동안 gradient가 소실됨. 이로 인해 네트워크가 전체 학습 단계에서 랜덤하게 초기화된 풀링 노드가 업데이트 되지 않고 학습 가능한 풀링 계층의 이점을 상실한다. 이 문제를 해결하기 위해 FC-layer를 사용한다. 이 FC-layer는 각 feature에 따라 kernel로 작동하고 원하는 수의 node를 출력한다. 또한 adaptive graph convolution을 사용하기 때문에 pooling은 graph를 절단하지 않는다.

3.2.3 Graph Unpooling

The unpooling layer used in our Graph U-Net is also different from Gao et al.’s gUnpool [5]. We use a transpose convolution approach in our unpooling layer. Similar to our pooling layer, we use a fully-connected layer and applied it on the transpose matrix of the features to obtain the desired number of output nodes, and then transpose the matrix again.

• Unpooling layer도 이전 논문과 다르다. 본 논문의 접근 방식은 unpooling layer에서 transpose convolution 접근 방식을 사용한다. Pooling layer와 비슷하게 FC-layer를 사용하고 원하는 수의 output node를 얻기 위해 FC-layer를 transpose matrix에 적용하여 다시 행렬을 transpose 시킨다.

3.3. Loss Function and Training the Model

Our loss function for training the model has three parts. We first calculate the loss for the initial 2D coordinates predicted by ResNet ($\mathcal{L}_{init2D }$). We then add this loss to that calculated from the predicted 2D and 3D coordinates ($\mathcal{L}_{2D}$ and $\mathcal{L}_{3D}$),

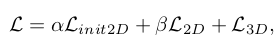
where we set α and β to 0.1 to bring the 2D error (in pixels) and 3D error (in millimeters) into a similar range. For each of the loss functions, we used Mean Squared Error.

• Network의 학습을 위한 loss function은 3가지이다. 처음에 ResNet을 통해 예측된 2D coordinate에 대한 loss를 계산한다. 그리고 refine한 2D coordinate에 대한 loss와 3D coordinate에 대한 loss를 추가한다. 각 loss function은 MSE를 사용하고, $\alpha, \beta$ 는 0.1로 설정한다.

4. Results

4.1. Datasets

FPHA, HO-3D 사용하였고, pre-training을 위해 ObMan dataset 사용

4.2. Implementation Details

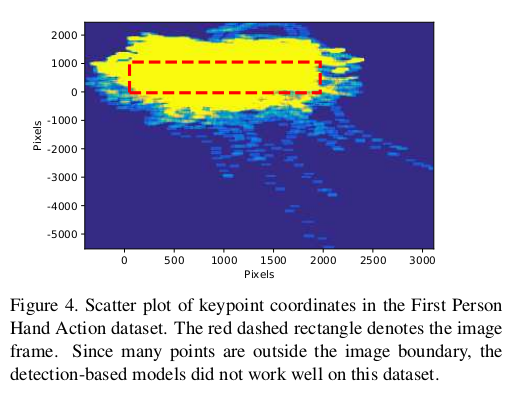
• Detection-based model을 사용할 경우 bounding box 밖에 joint가 있는 경우가 많아 regression-based model로 lightweight ResNet10을 사용하였음.

4.3. Metrics

Similar to [26], we evaluated our model using percentage of correct pose (PCP) for both 2D and 3D coordinates. In this metric, a pose is considered correct if the average distance to the ground truth pose is less than a threshold.

• 2D 및 3D 좌표 모두에 대해 correct pose (PCP) 백분율을 사용하여 model을 평가하였다. 이 메트릭에서, GT 포즈까지의 평균 거리가 threshold보다 작은 경우 올바른 것으로 간주한다.

4.4. Hand-Object Pose Estimation Results

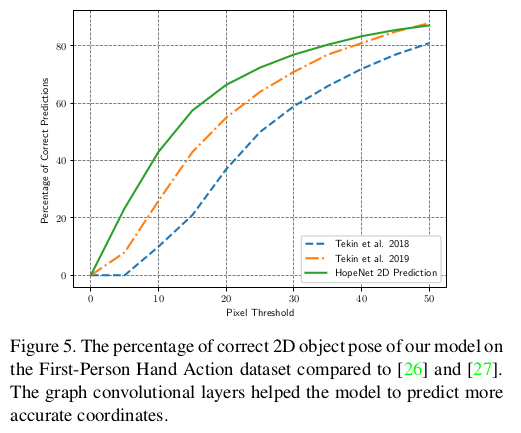
• FPHA dataset에 대해 object pose가 얼마나 올바른지에 대해서 측정하였는데 기존 SOTA 보다 더 좋은 성능을 내고있고, architecture가 lightweight하기 때문에 더 빠르며 graph convolution layer가 더 정확한 coordinate를 예측하기에 도움이 된다고 이야기 하고 있음.

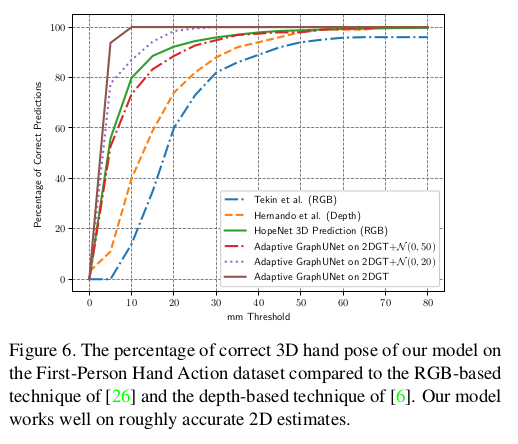
• 이는 FPHA의 3D pose에 대해서 metric을 측정하였음. 여기서도 더 좋은 결과를 보임. 이는 GT와 GT에 Gaussian noise를 섞은 데이터를 input으로 사용하였을 때의 결과이다. 전반적으로 잘 예측한 것을 보이는데, 이는 graph model이 효과적으로 keypoint coordinate로 부터 Gaussian noise를 잘 제거한다는 것을 알 수 있다. (Adaptive GraphUNet on 2DGT + ~)

• FPHA dataset에 대한 qualitative results이다. 색깔있는게 prediction이고, 검은색이 GT이다. 참고로, 제일 밑 row는 잘 안된 case이다.

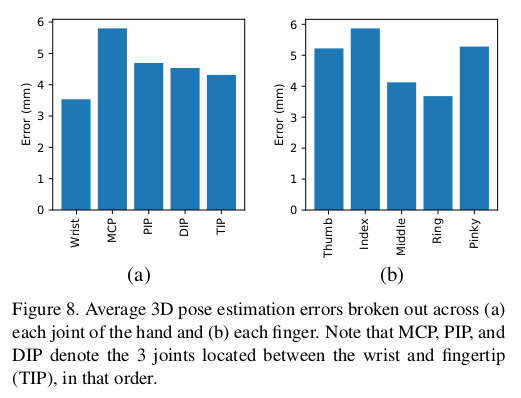
• 각 손가락과 hand의 joint 유형에 대한 2D에서 3D로의 converter의 error를 보여준다. (a)는 손의 각 joint, (b)는 finger에 걸쳐 분류된 pose estimation error이다. MCP, PIP, DIP는 손목과 fingertip 사이에 있는 3개의 관절을 순서대로 나타낸다.

• HO-3D 에 대한 결과는 논문에 적혀있는데 확인해보면 됨.

4.5. Adaptive Graph U-Net Ablation Study

To show the effectiveness of our U-Net structure, we compared it to two different models, one with three Fully Connected Layers and one with three Graph Convolutional Layers without pooling and unpooling.

• U-Net 구조의 효율성을 보여주기 위해 pooling 및 unpooling이 없는 3개의 FC-layer가 있는 model과 3개의 Graph Convolution layer가 있는 모델과 비교하였다. Table 1은 결과를 보여주는데, Adaptive graph U-Net이 다른 방법보다 큰 차이로 더 나은 성능을 보인다. 이 큰 차이는 U-Net 구조와 pooling 및 unpooling layer에서 비롯된 것으로 보인다.

• 이는 Graph pooling layer의 효과를 비교하기 위한 실험이다. 더 효율적인 학습 알고리즘 및 pooling 후에 그래프 절단이 생기지 않음으로써 논문에서 제시하는 pooling이 더 나은 성능을 보인다는 것을 알 수 있다.

Since we are using an adaptive graph convolution, the network learns the adjacency matrix as well. We tested the effect of different adjacency matrix initializations on the final performance, including: hand skeleton and object bounding box, empty graph with and without self-loops, complete graph, and a random connection of vertices. Table 3 presents the results of the model initialized with each of these matrices, showing that the identity matrix is the best initialization. In other words, the model seems to learn best when it finds the relationship between the nodes starting with an unbiased (uninformative) initialization.

• Adaptive graph convolution의 사용은 adjacency matrix을 학습시킨다. 저자는 최종 성능에 대한 다양한 adjacency matrix initialization의 효과를 테스트했다. 여기에는 hand skeleton, object bounding box, self-loop가 있거나 없는 빈 그래프, 완전 그래프, vertex가 랜덤하게 연결된 graph를 포함한다. Table 3은 이러한 각 행렬로 모델을 초기화한 결과를 보여주며, Identity matrix가 최상의 성능을 보여주는 initialization임을 보인다. 즉, 모델은 정보가 없는 초기화로 시작하는 노드 간의 관계를 찾을 때 가장 잘 학습하는 것으로 보인다. (네 번째 행의 “skeleton”은 사람 손의 실제 kinematic structure를 단순히 인코딩하는 adjacency matrix이다.)

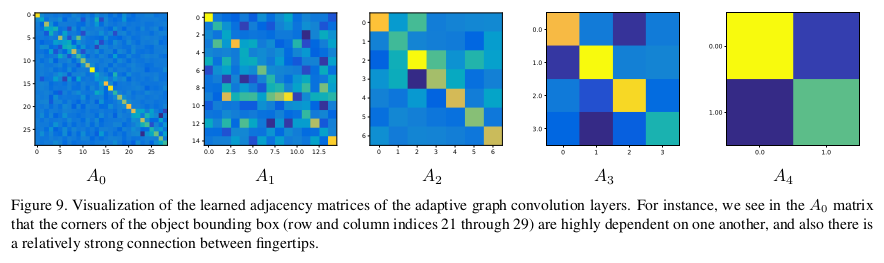
• Adaptive Graph Convolution layer의 학습된 adjacency matrix visualization. 예를 들면, $A_0$ matrix에서 object bounding box ((21, 21) ~ (29, 29))의 corner가 서로 크게 의존하고 있으며 또한 손가락 끝 사이에 상대적으로 강한 연결이 있음을 알 수 있음. (왼쪽 위와 색깔이 비슷함 / 이 케이스에서는 손과 물체가 연결되어 있지 않음)

4.6. Runtime

• 매우 빠름

5. Conclusion and Future Work

In this paper, we introduced a model for hand-object 2D and 3D pose estimation from a single image using an image encoder followed by a cascade of two graph convolutional neural networks. Our approach beats the state-of-the-art, while also running in real-time.

• 이 논문에서 두 개의 GCN 구조가 뒤따르는 image encoder를 사용하여 single RGB image에서 hand-object 2D, 3D pose estimation을 하는 model을 소개한다. 이는 real-time에서 작동하며 SOTA의 성능을 달성하였다.

Nevertheless, there are limitations of our approach. When trained on the FPHA and HO-3D datasets, our model is well-suited for objects that are of similar size or shape to those seen in the dataset during training, but might not generalize well to all categories of object shapes. For real-world applications, a larger dataset including a greater variety of shapes and environments would help to improve the estimation accuracies.

• 그럼에도 불구하고 논문의 접근 방식에는 한계가 있다. FPHA 및 HO-3D dataset에서 학습될 때 모델은 학습 중 데이터 셋에서 본 것과 크기 또는 모양이 유사한 물체에는 잘 적합하지만 물체 모양의 모든 범주에 잘 일반화되지 않을 수 있다. 실제 application에서 더 다양한 모양과 환경을 포함하는 더 큰 데이터셋이 estimation accuracy를 개선하는 데 도움이 될 것 이다.

Future work could include incorporating temporal information into our graph-based model, both to improve pose estimation results and as step towards action detection. Also, in addition to hand pose estimation, the Adaptive Graph U-Net introduced in this work can be applied to a variety of other problems such as graph completion, protein classification, mesh classification, and body pose estimation.

• Future work로는 graph-based model에 temporal 정보를 통합해 pose estimation 결과를 개선하고 action detection을 위해 한 단계로 통합하는 작업이 포함될 수 있다. 또한 Adaptive Graph U-Net은 hand pose estimation 외에도 graph completion, protein classification, mesh classification, body pose estimation 등 다양한 문제에 적용할 수 있다.

• 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.

Code

make_data.py → image는 path, point는 label값들이 들어있음.

ex) points3D-train → (11019, 29, 3)

Uploaded by N2T