논문 링크 : https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8578406
Abstract
In this paper, we investigate the problem of end-to-end 3D surface prediction. We first demonstrate that the marching cubes algorithm is not differentiable and propose an alternative differentiable formulation which we insert as a final layer into a 3D convolutional neural network. We further propose a set of loss functions which allow for training our model with sparse point supervision. Additionally, it learns to complete shapes and to separate an object’s inside from its outside even in the presence of sparse and incomplete ground truth.
1. Introduction
We propose Deep Marching Cubes (DMC), a model which predicts explicit surface representations of arbitrary topology. Inspired by the seminal work on Marching Cubes [29], we seek for an end-to-end trainable model that directly produces an explicit surface representation and optimizes a geometric loss function. Besides, this allows for separating inside from outside even if the ground truth is sparse or not watertight, as well as easily integrating additional priors about the surface (e.g., smoothness).
본 논문에서 제안하는 Deep Marching Cubes (DMC) 는 arbitrary topology에 대해 explicit surface representation을 예측하는 model이다. 저자는 Marching Cube로 부터 영감을 받아서 end-to-end 방식으로 학습가능한 model을 제시하였는데 이 model은 direct하게 explicit surface representation을 만들어내고, geometric loss function을 최적화 시킨다. 게다가, 이 model은 GT가 sparse하거나 완벽하지 않아도 내부와 외부를 분리할 수 있을 뿐만 아니라, surface에 smoothness와 같은 추가적인 prior를 쉽게 통합할 수 있다.
논문에서 제시하는 contribution은 다음과 같다.
- We demonstrate that Marching Cubes is not differentiable with respect to topological changes and propose a modified representation which is differentiable.
- Marching Cube가 topological change에 대해 미분 불가능함을 정의하고, 미분가능한 수정된 representation을 제안한다.
- We present a model for end-to-end surface prediction and derive appropriate geometric loss functions. Our model can be trained from unstructured point clouds and does not require explicit surface ground truth.
- surface prediction을 위한 end-to-end model을 제시하고, 적절한 geometric loss function을 도출한다. 제안된 모델은 unstructured point clouds에서 학습 가능하고, explicit surface GT를 필요로 하지 않는다.
- We propose a novel loss function which allows for separating an object’s inside from its outside even when learning with sparse unstructured 3D data.
- sparse한 비정형 3D data로 학습할 때도 object의 내부와 외부를 분리할 수 있는 novel한 loss function을 제시한다.
- We apply our model to several surface prediction tasks and demonstrate its ability to recover surfaces even in the presence of incomplete or noisy ground truth.
- 제시한 model을 여러 surface prediction task에 적용하고, 심지어 불완전 하거나 noisy한 GT가 있는 경우에도 surface를 잘 recover하는 능력을 실험을 통해 보여준다.
3. Deep Marching Cubes
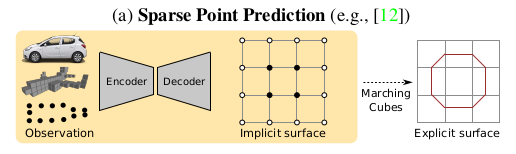
We tackle the problem of predicting an explicit surface representation (i.e., a mesh) directly from raw observations (e.g., a mesh, point cloud, volumetric data or an image). Existing works formulate this problem as the prediction of an intermediate signed distance representation using an auxiliary (typically ) loss [10, 35], followed by applying the Marching Cubes (MC) algorithm [29]. In this work we aim at making this last step differentiable, hence allowing for end-to-end training using surface based geometric loss functions.
- 저자는 mesh, point cloud, volumetric data 또는 image 같은 raw observation으로 부터 direct하게 explicit surface representation을 예측하는 문제를 다룬다. 기존 work는 이 문제를 loss와 같은 보조적인 loss를 사용해 intermediate signed distance representation의 예측으로 공식화한 다음 marching cube 알고리즘을 적용한다. 논문에서는 마지막 단계를 미분 가능하게 만드는 것을 목표로 하고, end-to-end 학습을 위해 geometric loss function 기반의 surface를 사용한다.
3.1 Marching Cubes
The Marching Cubes (MC) algorithm extracts the zero level set of a signed distance field and represents it as a set of triangles. It comprises two steps: estimation of the topology (i.e., the number and connectivity of triangles in each cell of the volumetric grid) and the prediction of the vertex locations of the triangles, determining the geometry.
- Marching Cube 알고리즘은 signed distance field의 zero level set을 추출하고 triangle set으로 표현한다. 이는 2가지 step으로 구성되어있는데, 첫 번째는 volumetric grid의 각 cell에 있는 triangle의 수와 연결성 등 topology를 estimation하는 것, 두 번째는 triangle의 vertex location을 예측하여 geometry를 결정하는 것이다.
More formally, let denote a (discretized) signed distance field obtained using volumetric fusion [8] or predicted by a neural network [10, 35] where denotes the number of voxels along each dimension. Let further denote the ’th element of where is a multi-index (i, j, k correspond to the 3 dimensions of ).
- 는 signed distance field, 즉 sdf라고 하자. 여기서 N은 각 차원에 따른 voxel 수이다. 그리고 은 의 ’th element인데 여기서 은 i, j, k의 multi-index이다.
As is a signed distance field, || is the distance between voxel and its closest surface point. Without loss of generality, let us assume that > 0 if voxel is located inside an object and < 0 otherwise. The zero level set of the signed distance field defines the surface which can be represented by means of a triangular mesh . This mesh can be extracted from using the Marching Cubes (MC) algorithm [29] which iterates (“marching”) through all cells of the grid connecting the voxel centers and inserts triangular faces whenever a sign change is detected.
- || 은 voxel 과 가장 가까운 surface point와의 거리이다. 일반성을 잃지 않고, 이 0보다 크면 voxel 이 object 안에 있다고 가정하고, 이 0보다 작으면 그 반대이다. SDF의 zero level set은 triangluar mesh 으로 표현될 수 있는 surface를 정의한다. 이 mesh 은 voxel 중심을 연결하는 grid의 모든 cell을 반복하고 sign change가 감지될 때마다 face를 삽입하는 marching cube 알고리즘을 사용하여 SDF로 부터 추출된다. 아래 figure를 보면 잘 이해할 수 있음.
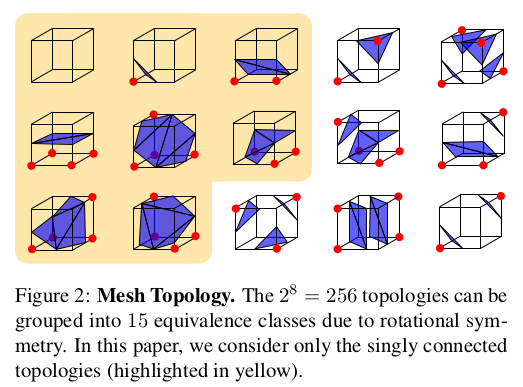
More specifically, MC performs the following two steps: First, the cell’s surface topology is determined based on the sign of at its 8 corners. can be represented as a binary tensor where each element represents a corner. The total number of configurations equals = 256, see Fig. 2 for an illustration. A vertex is created in case of a sign change of the distance values of two adjacent corners of the cell (i.e., corners connected by an edge). The vertex is placed at the edge connecting both corners.
- 더 정확히 MC는 2가지 스텝을 따른다. 먼저, cell surface topology T 는 8개의 코너에서 d_n 의 부호를 기반으로 결정된다. 그러면 전체 개수는 256개가 된다 아래를 참고하라. vertex는 cell에서 인접 코너의 distance value의 부호가 바뀔때 생성된다. vertex는 두 corner를 연결한 edge에 위치한다.
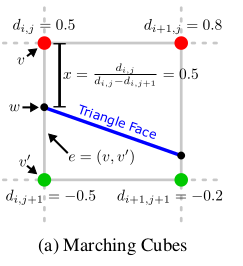
In a second step, the vertex location of each triangular face along the edge is determined using linear interpolation. More formally, let x ∈ [0, 1] denote the relative location of a triangle vertex w along edge where and are the corresponding edge vertices as illustrated in Fig. 3a.
- 두 번째로는 edge를 따라 triangular face의 vertex location은 linear interpolation을 사용하여 결정된다. edge를 두 점의 연결로 표현하는데 여기서 v를 기준으로 상대적인 location을 x로 표현한다. 예를 들면, x = 0 이면 w 라는 triangular face의 vertex가 v와 같고, x = 1 이면 v' 과 같다. Marching Cube algorithm에서 x를 구하는 식은 다음과 같은 함수의 해를 통하여 구하게 된다. (f(x)) 식)
Discussion: Given the MC algorithm, can we construct a deep neural network for end-to-end surface prediction? Indeed, we could try to construct a deep neural network which predicts a signed distance field that is converted into a triangular mesh using MC. We could then compare this surface to a ground truth surface or point cloud and backpropagate errors through the MC layer and the neural network. Unfortunately, this approach is intractable for two reasons:
- 토론: MC 알고리즘이 주어지면 종단 간 표면 예측을 위한 심층 신경망을 구성할 수 있습니까? 실제로 우리는 MC를 사용하여 삼각형 메시로 변환되는 부호 있는 거리 필드를 예측하는 심층 신경망을 구성하려고 시도할 수 있습니다. 그런 다음 이 표면을 실측 표면 또는 포인트 클라우드와 비교하고 MC 레이어와 신경망을 통해 오류를 역전파할 수 있습니다. 불행히도 이 접근 방식은 다음 두 가지 이유로 다루기 어렵습니다.
- d = d' 일 경우에 문제가 생기므로 학습 중 topological change를 막는다. 그러니, point cloud나 부분 mesh를 input으로 사용할 경우 학습 중에 topology를 알 수 없다. 그 대신에, 네트워크는 학습 중에 topology를 학습해야할 필요가 있다.
- observation은 인접 셀에만 영향을 준다. 즉 표면이 통과하는 셀에만 작용을 하는데, 이 때문에 기울기는 예측된 surface에서 더 멀리 떨어진 cell로 전파가 되지 않는다.
To circumvent these problems we propose a modified differentiable representation which separates the mesh topology from the geometry. In contrast to predicting signed distance values, we predict the probability of occupancy for each voxel. The mesh topology is then implicitly (and probabilistically) defined by the state of the occupancy variables at its corners. In addition, we predict a vertex location for every edge of each cell. The combination of both implicitly defined topology and vertex location defines a distribution over meshes which is differentiable and can be used for backpropagation. The second problem can be tackled by introducing appropriate loss functions on the occupancy and the vertex location variables.
- 이러한 문제를 피하기 위해 mesh topology를 geometry로부터 문제하는 미분 가능한 representation을 제안한다. signed distance value를 에측하는 것과 달리, 각 voxel에 대해 occupancy에 대한 확률을 예측한다. mesh topology는 corner의 occupancy variables에 상태에 의해 implicit하게 정의된다. 게다가, 각 cell에서 모든 edge에 대해 vertex location을 예측한다. implicit하게 정의된 topology와 vertex location의 조합은 미분 가능하고 backpropagation에 사용될 수 있는 mesh를 정의한다. 두 번째 문제는 적절한 loss를 도입하여 해결할 수 있다.
3.2 Differentiable Marching Cubes
Let O ∈ (voxel grid dimension) denote the occupancy field and let X ∈ denote the vertex displacement field predicted by a neural network (see Section 3.3 for details on the network architecture). Let ∈ [0, 1] denote the n’th element of O, representing the occupancy probability of that voxel with o = 1 if the voxel is occupied. Similarly, let ∈ [0, 1] 3 denote the n’th element of X, representing the displacements of the triangle vertices along the edges associated with .
- 유사하게, ∈ [0, 1] 3 가 과 관련된 모서리를 따라 삼각형 꼭짓점의 변위를 나타내는 X의 n번째 요소를 나타내도록 합니다.
The topology can be implicitly defined via the occupancy variables. We consider the predictions of the neural network ∈ [0, 1] as parameters of a Bernoulli distribution.
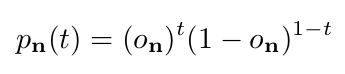
where t ∈ {0, 1} is a random variable and is the probability of voxel n being occupied (t = 1) or unoccupied (t = 0).
- voxel n이 occupied 되었는지 아닌지에 대한 확률이 이다.
Let now { , . . . ,} denote the = 8 occupancy variables corresponding to the 8 corners of the n’th grid cell.
- 그리고 부터 까지는 8개의 occupancy variables를 포함하는데 n'th grid cell의 corner와 일치한다.
Let further T ∈ denote a binary random tensor representing the topology. The probability for topology T at grid cell n is the product of the 8 occupancy probabilities at its corners
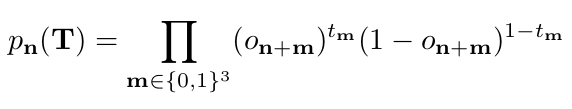
- 더 나아가 T는 topology를 나타내는 binary random tensor를 나타낸다. 그리드 셀 n 에서 topology T에 대한 확률은 코너에 있는 8개의 occupancy 확률의 곱이다.
Note that jointly with the vertex displacement field X, the distribution over topologies (T) at cell n defines a distribution over triangular meshes within cell n. Considering all cells n ∈ T we obtain a distribution over meshes in the entire grid as (3) where T = {1, . . . , N − 1} and the vertex displacements X are fixed to the predictions of the neural net.
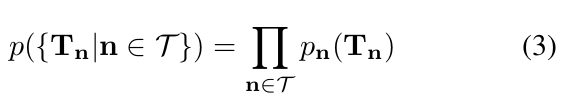
- vertex displacement field X와 셀 n의 topology 에 대한 분포는 triangular mesh에 대한 distribution을 정의한다. 전체 cell을 고려하면 전체 gird mesh에 대한 분포를 얻을 수 있다.
Remark: While the total number of possible topologies within a voxel is = 256, many of them represent disconnected meshes. As those are unlikely to occur in practice given a fine enough voxel resolution, in this paper we only consider the 140 singly connected topologies (highlighted in yellow in Fig. 2) and renormalize (2) accordingly.
- disconnected mesh가 충분히 정밀한 voxel 해상도에서 실제로는 잘 발생하지 않으니 하나씩 연결된 것들(노란색) 만 고려한다.
3.3 Network Architecture
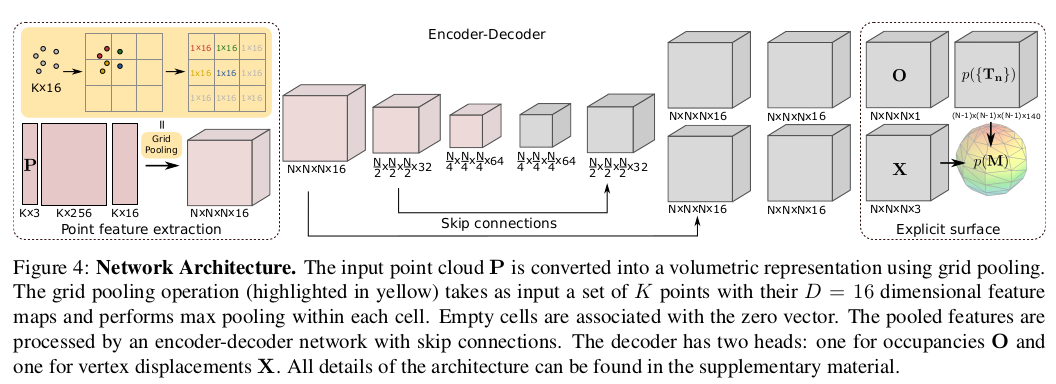
The encoder extracts features from the raw observations and the decoder predicts an explicit surface. In this paper we consider a 3D point cloud with K points as input. However, note that the encoder could be easily adapted to other types of observations including 3D volumetric information or 2D images.
- Encoder는 observation으로부터 feature를 추출하고 decoder는 explicit surface를 예측한다. 이 논문에서 K개의 point를 input으로 하는 3차원 point cloud P를 고려한다. 그러나 인코더는 3D volumetric information 또는 2D 이미지를 포함한 다른 유형의 observation에 쉽게 적용할 수 있다. 본 논문의 Encoder Architecture는 PointNet의 변형이다.
network 구조는 figure4와 같다. 먼저, 각 point로 부터 FC layer를 사용해 local feature vector를 추출한다. 그 다음, voxel에 속하는 모든 point를 하나의 set으로 그룹화하고 이 voxel 내에서 grid pooling을 적용한다. 논문에서는 grid pooling의 input으로 16 dimensional feature map을 받아 각 cell마다 max pooling을 적용한다고 한다. 빈 cell은 zero vector이다. 그 다음 이 feature를 skip connection과 함께 encoder-decoder network구조를 지나게 한다. decoder는 2가지의 head를 가지는데, 하나는 occupancy를 위한 것이고, 하나는 vertex displacement를 위한 것이다. 이를 이용해 Explicit surface를 만든다.
3.4 Loss Functions
At training time, our goal is to minimize the distance between the ground truth point cloud and the predicted surface mesh M. Note that our model predicts a distribution over surface meshes p(M) thus we minimize the expected surface error. We add additional constraints to regularize the occupancy variables and the smoothness of the estimated mesh.
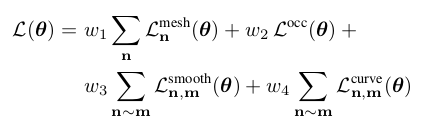
θ represents the parameters of the neural network in Fig. 4, {} are the weights of the loss function and n ∼ m denotes the set of adjacent cells in the grid.
Point to Mesh Loss:
Let Y denote the set of observed 3D points (i.e., the ground truth) and let ⊆ denote the set of observed points falling into cell n. As our model predicts a distribution of topologies (T) and hence also meshes at every cell n, we seek to minimize the expected error with respect to this distribution.
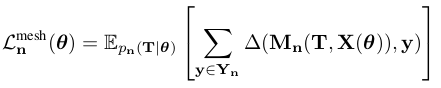
where y ∈ R is an observed 3D point, M (T, X) represents the mesh induced by topology T and vertex displacement field X at cell n, and ∆(M, y) denotes the point-to-mesh distance if .
- Y는 gt, Y_n은 cell n에 있는 Y의 point subset. 모델은 topology 의 분포를 예측하고 모든 cell n에서 mesh를 생성하므로 이 분포와 관련하여 예상되는 오류를 최소화하려고 한다. 수식에서 y는 관찰된 3D point, M_n은 topology T와 cell n에서의 vertex displacement field X로 부터 유도된 mesh이고, 델타는 point-to-mesh distance이다. 여기서 point-to-mesh distance는 y와 가장 가까운 triangle을 찾아 euclidean distance를 이용해 계산된다.
That is, surface predictions far from the observations are not penalized as long as all observations are covered by the predicted surface mesh. We therefore add a small constant loss on all non-empty topologies for cells without observed points. Moreover, we introduce additional loss functions that prefer simple solutions in the following paragraphs.
- observation에서 멀리 떨어진 surface 예측은 페널티를 받지 않는 문제가 있다. 그래서 관찰된 점이 없는 cell에 대해 비어 있지 않은 모든 topology에 작은 constant loss를 추가한다. 이를 다음 단락에서 소개한다.
Occupancy Loss:
The occupancy status is ambiguous when considering unstructured 3D point clouds as observations.
- 구조화되지 않은 3D point cloud를 observation으로 고려할 때 occupancy status가 모호하다.
However, we observe that for most scenes objects are surrounded by free space, thus we can safely assume that the 6 faces of the cube bounding the 3D scene are unoccupied.
- 대부분의 scene에서 object가 free space로 둘러싸여 있다는 것을 발견하여 3D scene을 경계 짓는 cube의 6면이 비어있다고 안전하게 가정할 수 있다.
Defining a prior for occupied voxels is more challenging. One could naı̈vely assume that the center of the bounding cube must be occupied, yet this is not true in general. Thus, we relax this assumption by encouraging a sub-volume inside the scene to be occupied.
- voxel의 occupy에 대한 prior를 정의하는 것은 더 어렵다. bounding cube의 중심이 채워져야 한다고 가정할 수 있지만 일반적으로 그렇지 않다. 따라서 scene 내부의 sub-volume을 차지하도록 권장하여 위의 가정을 완화한다. 그 식은 다음과 같다.
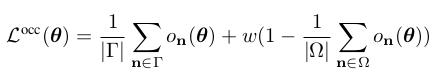
여기서 감마는 scene cube에 대한 boundary이고 오메가는 cube 내부의 sub-volume이다.
Minimizing the first term of (6) encourages the boundary voxels to become unoccupied. Minimizing the second term enforces a region within the scene cube to become occupied depending on the adaptive weight w, which decreases with the number of high confident occupied voxels in the scene.
- 첫 번째 term 을 최소화하면 boundary voxel이 unoccupied 하게 된다. 두 번째 term을 최소화하면 scene cube 내의 영역이 가중치 w에 따라 occupied 되도록 하며, w는 scene에서 high confident occupied voxels의 수에 따라 감소한다.
Smoothness Loss:
To propagate occupancy information within the volume, we therefore introduce an additional smoothness loss. In particular, we assume that the majority of all neighboring voxels take the same occupancy state. This assumption is justified by the fact that transitions happen only at the surface of an object (covering the minority of voxels).
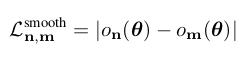
- volume 내 occupancy 정보를 전파하기 위해 추가적인 smoothness loss를 도입한다. 특히, 모든 이웃 voxel의 대다수가 동일한 occupancy 상태를 취한다고 가정한다. 이 가정은 transition이 object의 surface에서만 발생한다는 사실에 의해 정당화된다.
Curvature Loss:
Similarly to the smoothness loss on the occupancy variables we can encourage smoothness of the predicted mesh geometry. This is particularly important if the ground truth point cloud is sparse and noisy as assumed in this paper. We therefore add a curvature loss which enforces smooth transitions between adjacent cells by minimizing the expected difference in normal orientation:
- occupancy variables에 대한 smoothness loss와 비슷하게 예측된 mesh geometry에 대해 smoothness를 북돋을 수 있다. 이는 이 논문에서 가정한 것 처럼 gt point cloud가 sparse하고 noisy할 경우에 특히 중요하다. 따라서 수직 방향에서 예상되는 차이를 minimizing하여 인접셀 간의 부드러운 transition을 하게 하는 curvature loss를 추가한다.
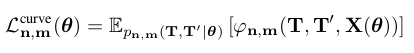
Here, is the joint distribution over the topologies of voxel n and voxel m. Furthermore, φ(·) denotes a function which returns the squared distance between the normals of the faces in cell n and m which are connected by a joint edge, and 0 if the faces in both cells are not topologically connected.
- 여기서, 는 voxel n과 voxel m에 대한 joint distribution이다. 게다가, φ(·)는 cell n과 m에서의 joint edge를 통해 연결된 face 법선 사이의 squared 거리를 반환하고, 두 cell에서의 face가 위상학적으로 연결 되있지 않을 경우 0이다.
4. Experimental Evaluation
4.1. Model Validation in 2D
We rendered silhouettes of 1547 different car instances from ShapeNet [5], which we split into 1237 training samples and 310 test samples. We randomly sampled 300 points from the silhouette boundaries which we feed as input to the network. We use a voxel grid of size N × N × N with N = 32 throughout all of our experiments.
- ShapeNet에서 서로 다른 1547개의 car instance의 실루엣을 렌더링했고, 이를 train set으로 1237개, test set은 310개로 나누었다. network의 input으로 300개의 point를 실루엣 boundary에서 랜덤하게 sampling하였다. N x N x N voxel grid를 사용하였고, 실험에서는 N = 32로 두고 하였다. Measure로는 chamfer distance, hamming distance, accuracy, completeness을 사용함. 모든 measure는 거리로 지정되므로 낮을 수록 좋음.
Ablation Study:
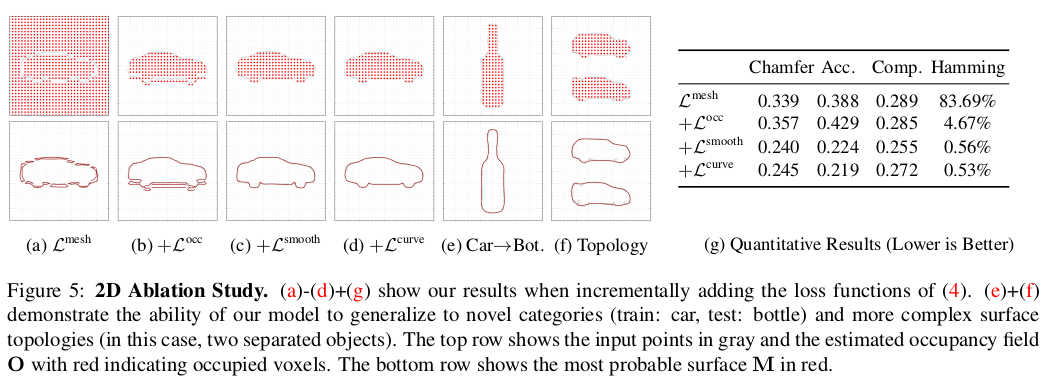
We first validate the effectiveness of each component of our loss function in Fig. 5. Starting with the point to mesh loss , we incrementally add the occupancy loss , smoothness loss and curvature loss .
- 4가지의 Loss를 한 개씩 추가하며 성능 측정 해봄.
Using only , the network predicts multiple surfaces around the true surface and fails to predict occupancy (a). Adding the occupancy loss allows the network to separate inside from outside, but still leads to fragmented surface boundaries (b). Adding the smoothness loss , removes these fragmentations (c). The curvature loss further enhances the smoothness of the surface without decreasing performance.
- 를 사용하면 실제 surface 주변의 여러 surface를 예측하지만 occupancy를 예측하지 못한다. 를 추가하면 network가 내부와 외부를 분리할 수 있다. 하지만 여전히 부서져있는 surface boundary를 생성한다. 를 추가하면 이러한 fragmentation을 없앨 수 있다. 는 성능의 감소 없이 surface에 대한 smoothness를 강화한다.
Generalization & Topology:
To demonstrate the flexibility of our approach, we apply our model trained on the category “car” to point clouds from the category “bottle”. Fig. 5f shows that our method, trained and tested with multiple separated car instances also handles complex topologies, correctly separating inside from outside, even when the center voxel is not occupied, validating the robustness of our occupancy loss.
- model의 flexibility를 정의하기 위해 car에서 model을 훈련시키고 bottle을 inference한 것을 보이는게 (e) 이다. (f)는 여러개의 분리된 자동차 인스턴스로 훈련하고 테스트된 방법이 복잡한 토폴로지(여기서는 두 개의 분리된 물체)를 처리해 center voxel이 occupy되지 않은 경우에도 내부와 외부를 올바르게 잘 분리한다는 것을 보인다.
Model Robustness:
In this section, we demonstrate that our method is able to reconstruct surfaces even in the presence of noisy and incomplete observations.
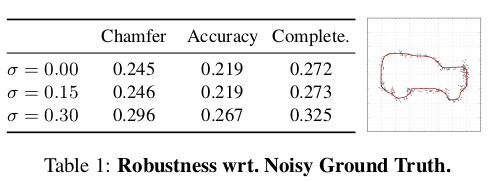
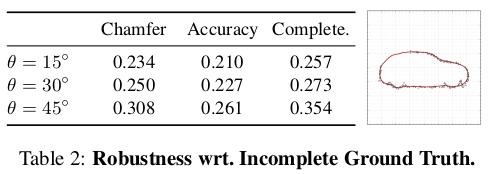
시그마 : noisy한 정도
세타 : 최대 세타 각도 범위 내 정보 사용 X
4.2. 3D Shape Prediction from Point Clouds
In this section, we verify the main hypothesis of this paper, namely if end-to-end learning for 3D shape prediction is beneficial wrt. regressing an auxiliary representation and extracting the 3D shape in a postprocessing step.
- 이 섹션에서는 이 논문의 주요 가설, 즉 3D shape prediction을 위한 end-to-end learning이 postprocessing 단계에서 보조의 representation을 regressing하고 3D shape을 추출하는데 유익한지 검증한다.
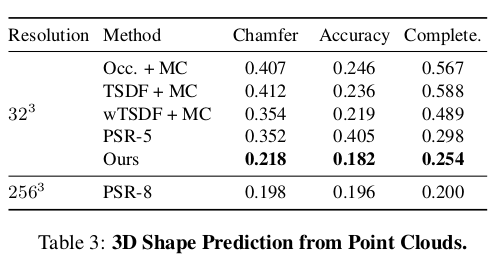
- 모든 예측된 mesh는 128 x 128 x 128 resolution에서 TSDF를 통해 추출된 ground truth mesh와 비교된다.

- qualitative results
- 제일 밑에 2줄은 실패한 case로 분류됨.
5. Conclusion
We proposed a flexible framework for learning 3D mesh prediction. We demonstrated that training the surface prediction task end-to-end leads to more accurate and complete reconstructions. Moreover, we showed that surface-based supervision results in better predictions in case the ground truth 3D model is incomplete. In future work, we plan to adapt our method to higher resolution outputs using octrees techniques [18,36,39] and integrate our approach with other input modalities like the ones illustrated in Fig. 1.
- 3D mesh prediction을 위한 유연한 framework 제시. surface prediction task를 위해 end-to-end 방법의 학습은 더 정확하고 완전한 reconstruction을 이끈다. 게다가, ground truth 3D model이 불완전 할 때 surface 기반의 supervision은 더 나은 예측 결과를 보여준다. future work로는 high resolution output, 다른 입력 방식과 접근 방식의 통합을 제시하였다.
- 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.
Uploaded by N2T
'Paper Summary' 카테고리의 다른 글
| Dynamic Plane Convolutional Occupancy Networks, WACV’21 (1) | 2023.03.26 |
|---|---|
| Occupancy Networks: Learning 3D Reconstruction in Function Space, CVPR’19 (1) | 2023.03.26 |
| Generative Adversarial Networks, NIPS’14 (0) | 2023.03.26 |
| DCGAN, ICLR’16 (0) | 2023.03.26 |
| Graph Attention Networks, ICLR’18 (0) | 2023.03.26 |