1. Introduction
In this work, we propose Dynamic Plane Convolutional Occupancy Networks, an implicit representation that enables accurate scene-level reconstruction from 3D point clouds. Instead of learning features on three pre-defined canonical planes as in [28], we use a fully-connected network to learn dynamic planes, on which we project the encoded per-point features. We systematically investigate the use of up to 7 learned planes and demonstrate progressive improvements by increasing the number of learned planes in our experiment.
- 논문은 3D point cloud로 부터 정확한 scene-level reconstruction을 가능하게 하는 implicit representation인 Dynamic Plane Convolutional Occupancy Networks를 제시한다. Convolutional Occupancy Network와 다르게 미리 정의된 3 개의 canonical planes에서 features를 학습하는 대신, encoding된 point 별 feature를 projection하는 dynamic planes을 학습하기 위해 fc network를 사용한다. 저자는 최대 7개의 학습된 평면의 사용을 체계적으로 조사하고 학습된 평면의 수를 늘려 점진적 개선을 보여준다.
Contribution
- feature 학습에서 deep neural network를 활용하여 unoriented point cloud로 부터 3D surface reconstruction task에 가장 적합한 plane을 예측하는 것
- object 와 scene level의 3D surface reconstruction task에 대해 기존 sota 방식 대비 우월성
- 실험에서 dynamic plane의 분포에 대한 다양한 관찰 제공
In addition, we exploit the use of positional encoding proposed in [24], which maps the low dimensional 3D point coordinates to higher-dimension representations with periodic functions under various frequencies. Additionally, we formulate a similarity loss function to govern the orientations of dynamic planes to orient in diverse directions.
- 추가적으로 positional encoding을 활용하여 low dimensional 3D point coordinate를 다양한 frequency에서 periodic function을 사용해 high dimension representation으로 매핑한다. 그리고 dynamic plane의 방향을 다양한 방향으로 제어하기 위해 similarity loss function을 공식화한다.
3. Method
Our goal is to reconstruct 3D scenes with fine details from noisy point clouds. To this end, we first encode the input point clouds into 2D feature planes, whose parameters are predicted by a fully-connected network. These feature planes are then processed using convolutional networks and decoded into occupancy probabilities via another shallow fully-connected network. Fig. 1 illustrates the overall workflow of the proposed method.
- network의 목표는 noisy point cloud로 부터 세밀한 detail을 잘 살린 3D scene reconstruction이다. 이를 위해 첫 번째로 input point cloud를 fc network를 통해 파라미터가 예측되는 2D feature plane으로 encoding하는 것이다. 이 feature는 그 후에 convolution network를 통해 처리되고 다른 shallow fc network를 통해 occupancy probability로 decoding된다. Fig. 1이 제안된 method의 전반적인 workflow를 제시한다.

- Figure 설명 : N 개의 input point cloud가 ResNet PointNet에 의해 point 별 feature로 encoding되는데 이 때 feature dimension은 D이다. → Encoded features dimension이 N x D. 동시에 shallow plane predictor network는 input point cloud에서 L개의 dynamic plane과 plane별 feature를 학습한다. 그리고 인코딩된 모든 point 별 feature에 plane feature를 sum한다.
- 다음으로, 합쳐진 feature가 dynamic plane에 projection된다. 그 다음 projection된 plane feature는 plane 간에 weight를 공유하는 U-Net을 사용하여 처리된다. Decoding 단계에서 uniform하게 sampling된 점 p의 occupancy는 bi-linear interpolation에 의해 query된 local 평면 feature로 조절되는 얕은 fc network에 의해 예측된다.
3.1. Encoder

- Figure.2 설명 : point 별 feature를 추출하기 위해 ResNet PointNet을 사용한다. 윗단에 simple PointNet 으로 구성된 plane predictor network를 추가하여 dynamic plane parameter를 예측한다.
Point cloud encoding:
Given a noisy point cloud, we first form a feature embedding for every point with ResNet PointNet [23], in which we perform local pooling according to the predefined plane resolution [28]. We are applying a rather simple network here for the proof of concept, but other advanced feature extractors, e.g., PointNet++ [31] or Tangent Convolution [33], can also be used.
- noisy point cloud가 주어지면 ResNet PointNet을 사용하여 모든 point에 대한 feature embedding을 형성하고 여기서 미리 정의된 plane resolution에 따라 local pooling을 수행한다. 여기서는 다소 간단한 네트워크를 적용하고 있지만 PointNet++ 또는 Tangent Convolution과 같은 다른 고급 feature extractor도 사용할 수 있다.
Dynamic plane prediction:
Having the point-wise features, we can then construct the planar features. Mathematically, a plane is defined by a normal vector n = (a, b, c) and a point (x, y, z) which a plane passes through: ax + by + cz = d. Peng et al. [28] simply project features onto canonical planes, i.e., 3 planes aligned with the axes of the coordinate frame, x = 0, y = 0, z = 0. Unlike [28], we introduce another shallow fully-connected network to regress the plane parameter (a, b, c).
- point-wise feature를 갖고 있으면 planar feature를 구성할 수 있다. 수학적으로 plane은 normal vector와 point를 통해 정의할 수 있는데, 그 식은 ax + by + cz = d 와 같다. [28] (Convolutional Occupacny Network) 논문에서는 단순하게 axes에 따른 3개의 plane을 사용하였다. 하지만 본 논문에서는 이와 다르게 shallow fc network를 추가하여 plane parameter (a, b, c)를 regression한다. 이는 Figure.2 의 위쪽 branch와 같다.
We perform max pooling globally on all points in the point cloud because a global context is needed to search for the proposal of the best possible planes. Since different input point clouds might be predicted with different planes, we call this process dynamic plane prediction. Note that we directly set the intercept of the plane d to 0 because the shifts along the normal direction do not change the feature projection process.
- 가능한 best plane을 찾으려면 global context가 필요하기 때문에 point cloud의 모든 point에 대해 globally하게 max pooling을 수행한다. 논문에서는 다른 input point cloud가 다른 plane을 예측하므로 이를 dynamic plane prediction이라고 부른다. 그리고 논문에서는 plane 식의 d, 즉 intercept를 0으로 설정하는데, 이는 평면이 법선벡터 방향을 따라 움직여도 feature projection 과정이 변하지 않기 때문이라고 한다.
After the prediction of plane parameters, we pass it through one layer of FC to obtain a feature for every dynamic plane. This feature is expanded, matching the number of input point cloud and summed up with the last layer of ResNet PointNet with respect to the individual dynamic plane, and thus we call it the plane-specific feature. Our main intention is to allow backpropagation into the plane predictor network, but we also empirically find that this individual summation operation improves the reconstruction quality. One possible reason is that it allows the networks to learn varying emphasis over the feature dimension of the last layer of ResNet PointNet with respect to the individual dynamic plane.
- plane parameter를 예측한 후, 한 개의 FC layer를 통과시켜 모든 dynamic plane에 대한 feature(fig.2 에 plane-specific feature라고 적혀있음.)를 얻는다. 이 feature는 input point cloud의 수와 일치하게 확장되고 개별 dynamic plane에 대해 ResNet PointNet의 마지막 layer와 합산되므로 이를 plane-specific feature라고 한다. 저자의 주요 의도는 plane predictor network로 역전파를 허용하는 것이지만, 경험적으로 이 개별 합산 연산이 reconstruction quality를 향상시킨다는 것도 발견했다. 이를 가능하게 하는 이유는 network가 개별 dynamic plane과 관련하여 ResNet PointNet의 마지막 layer feature dimension에 대해 다양한 강조점을 학습할 수 있기 때문이다.
Once having the predicted plane parameters, we project the summed-up features onto the dynamic planes with a defined size of H × W grids and apply max pooling for the features falling into the same grid cell.
- 예측된 plane parameter가 있으면 합산된 feature를 정의된 size의 H x W grid로 projection하고 동일한 grid cell에 속하는 feature에 대해 max pooling을 적용한다.
Planar projection:
In order to project the encoded features to the dynamic planes, whose normals can point to any directions, we sequentially apply basis change, orthographic projection, and normalization to always keep them inside H × W grids. Denoting the three basis vectors of canonical axes, i, j, k, where k is the basis vector of the ground plane and n is the learned plane normal, those operations are detailed as follows and illustrated in Fig. 3.

- normal vector가 모든 방향을 가리킬 수 있는 dynamic plane에 encoding된 feature를 projection하기 위해 basis change, orthographic projection, normalization을 순차적으로 적용하여 항상 H x W grid 내부에 유지하게한다. 세 가지의 canonical axis를 i, j, k라고 하며 k는 ground plane의 basis vector이고 n은 학습된 plane의 normal vector이다. 이러한 작업은 Fig.3에 설명되어있다.
To perform basis change, we normalize n into a unit vector n̂ and obtain the rotation matrix R that aligns k with n̂. Let v = = k × n̂, the rotation matrix R is defined as:

where [v] is the skew matrix:

- basis change를 위해 n을 unit vector n̂ 으로 normalization을 하고, k를 n̂에 정렬하는 rotation matrix R을 얻는다. (Fig.3에 Plane coordinate 보면 K가 normal과 같아짐.) v를 다음과 같다고 하였을때 rotation matrix R은 식 (1)과 같이 정의가 된다.
With the rotation matrix R, we rotate the axes i and j to obtain and . Now, the vectors , and n̂ are orthogonal to each other, serving as the basis of the predicted plane coordinate system.
- rotation matrix R을 사용해서, axes i와 j를 , 를 얻기위해 사용한다. 벡터 , 그리고 n̂ 은 서로 직교 상태이며, 예측된 coordinate system의 basis가 된다. (Fig.3 보면 됨)
Next, we convert point coordinates from the world coordinate to the plane coordinate system and project the features orthographically to the predicted plane (”new ground plane”). However, as our dynamic plane can orient to any direction, the orthographic projection of a point far from the centroid of 3D space might fall outside the H × W grids.
- 다음으로, point 좌표를 global system에서 plane coordinate system으로 변환하고 feature를 예측 plane(즉, new ground plane)으로 orthogonal하게 projection한다. 그러나, dynamic plane이 모든 방향으로 향할 수 있으므로, 3D 공간의 centroid 에서 멀리 떨어진 점의 orthogonal projection이 H x W grid 외부에 떨어질 수 있다.
To ensure all possible points after orthographic projection are inside the grids, we divide the coordinates after projection by a normalization constant c ≥ 1. To find c, we first convert and to be inside the positive octant by taking their absolute values and . Next, we obtain orthogonal projections of the vector 1 = [1, 1, 1] to and :
- 이를 grid 내부에 있도록 하기 위해 projection 후 좌표를 1이상의 normalization constant c로 나눈다. 이 c를 찾으려면 먼저 와 를 절댓값화 하여 positive octant(양의 8진법)안에 있도록 변환한다. 그 다음으로 and 에 대한 벡터 1의 orthogonal projection을 얻는다. 그 식은 다음과 같다.
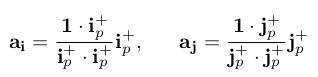
Subsequently, we set c to be the maximum value between the lengths of these two projected vectors, c = max(||, ||). The point coordinates under the plane coordinate system are divided by c so that all points lie inside the dynamic plane, where the point features are stored.
- 그 후, c 값은 방금 구한 , 값 사이의 최대값으로 설정한다. 이를 이용해 projection된 point들이 dynamic plane 내부에 놓이도록 한다.
3.2. Decoder
The goal of the decoder is to obtain the occupancy prediction of any point p ∈ given the aggregated planar features. Similar to how we project features in the encoder, we project p onto all dynamic planes. Next, we query the feature through bilinear interpolation of the planar features encoded at the four neighboring plane grids.
- Decoder의 목표는 평면 feature가 주어지면 어떤 point 에 대해서 occupancy prediction을 얻는 것이다. encoder에서 feature를 projection 하는 방법과 비슷하게, p를 모든 dynamic plane에 투영한다. 그 뒤에 4개의 인접한 평면 grid에서 encoding된 평면 feature에 대해 bilinear interpolation을 통해 feature를 쿼리(추정)한다.

Occupancy Prediction:
Given an input point cloud x, we predict the occupancy of p based on the feature vector at point p, denoted as ψ(p, x):

- input point cloud x가 주어지면, point p에 대한 feature vector에 기반하여 p에 대한 occupancy를 예측한다. 이에 대한 식은 위와 같다. (Convolutional Occupancy Network와 같은 형태)
3.3. Training and Inference
- 학습 시에는 occupancy prediction 과 ground truth에 대해 binary cross-entropy 적용, 그 후 Multi-resolution IsoSurface Extraction (MISE)를 사용하여 mesh를 구성한다.
3.4 Positional Encoding
- neural network를 통과시키기 전에 high-frequency 함수를 사용하여 input을 더 높은 차원의 feature에 mapping 하면 high-frequency variation을 포함하는 데이터를 더 잘 맞출 수 있다고 다른 논문에서 제시하였고, 이에 대한 positional encoding function은 다음과 같음.

- 여기서 L은 frequency band(주파수 대역) 즉, 주파수의 진폭이다. Table.1 에서 볼 수 있듯이 positional encoding이 일반화 성능에 영향을 미치고 있음을 알 수 있음. 특히, input 3D 좌표에 대한 positional encoding을 적용한다. L을 10으로 설정하면 input point cloud x와 query point p를 에서 으로 mapping함. (x, y, z 각 좌표가 20개씩으로 되는듯 함)

4. Experiments
- object-level reconstruction을 위해 ShapeNet에서 실험, scene-level reconstruction을 위해 synthetic indoor scene에서 실험
Metrics:
- Volumetric IoU (higher)
- Chamfer- (lower)
- Normal Consistency (higher) # mesh normal 과의 acc나 completeness 측정
- F-score (higher)
4.1. Object-Level Reconstruction
We follow [28] and uniformly sample 2048 points. We use a plane resolution of 64 2 and U-Net with a depth of 4. We run experiments with different combinations of canonical and dynamic planes. The results are summarized in Table 1.
- 저자가 제시한 방법중 여러 method에서 sota 달성, 비슷한 양의 GPU memory 사용. dynamic plane의 개수를 늘릴 수록 점진적인 성능향상 관찰함. positional encoding 썼을 때가 전부 성능이 좋았음. 수렴성도 더 빠름.

Observation on plane distribution:
Here, we discuss our observations on the distribution of the predicted dynamic planes. In the case of 3 dynamic planes, our network predicts three canonical planes for all objects. In the case of 5 and 7 dynamic planes, there are combinations of flipping sets of normals (e.g. one normal pointing upward and the other downward). Such flipping sets of normals are equivalent to applying a horizontal flip on the projected encoded features.
Similarity loss:
To test whether having diverse plane normals that are neither aligned nor flipping to each other can have a significant impact on the model performance, we try another variant where we restrict the learned plane normals to be diverging by adding a pairwise cosine similarity loss among plane normals.
- 서로 align 되거나 flipping 되지 않은 다양한 plane normal이 모델 성능에 상당한 영향을 미칠 수 있는지 여부를 테스트하기 위해 plane normal 간에 pairwise cosine similarity를 추가하여 학습된 plane normal이 발산하도록 규제하는 또 다른 변형을 시도한다.

- 는 pairwise plane normal pair 사이의 각도이고, M은 전체 pair의 개수이다. plane normal이 발산하도록(평면이 더 다양해짐) 하기위해, d = 10으로 세팅하는데 이는 < 45 또는 > 135 일때 similarity loss가 페널티를 주기 시작한다. 여기에 예측된 occupancy에 대한 binary cross-entropy loss를 추가한다.

- 본 논문에서는 C를 10 x M 으로 두었다. 3개의 평면 쓸때는 canonical axes와 거의 동일한 plane set이다.
Adding more planes, e.g. in 5 and 7 dynamic planes, gives predicted planes whose normals diverge from the canonical axes without any flipping or redundant set where slight variations between objects are observed.
- 5개나 7개 정도와 같이 더 많은 plane을 추가하면 object 간의 약간의 변동이 관찰되는 flip 또는 중복 세트 없이 canonical axes에서 normal이 벗어나는 예측 plane을 얻을 수 있다.

- 개별 object의 모양에 따라 달라질 수 있는 plane을 학습하는 network의 능력을 볼 수 있는데, 성능 면에서는 개선이 거의 또는 전혀 없다. Figure 6의 왼쪽에서는 normal의 위치를 보여준다. 오른쪽은 normal이 약간 변한 분포인데 이 작은 변화 내에서 다른 global structure를 가진 object가 다른 영역을 선호하는 것으로 관찰됨. (즉, normal의 변화는 약간이지만 structure는 크게 달라짐)

- similarity loss를 사용하면 dynamic plane을 많이 사용할 경우에 일반화가 더 잘됨. 위 figure는 object를 회전시켰을 때의 결과임.
4.2. Scene-Level Reconstruction
For the scene-level experiment, we uniformly sample 10,000 points from the ground truth meshes as input and apply Gaussian noise with a standard deviation of 0.05. During training, we query the occupancy probability of 2048 points.
- scene-level 실험에서는, 10,000개의 point를 gt mesh로부터 uniform하게 sampling하여 input으로 사용하고 Gaussian noise를 사용함. 학습 동안, 2048개의 point에 대해 occupancy probability를 쿼리함.

- 이 때의 실험에서는 similarity loss를 적용한 것을 기본으로 두었는데, 이는 similarity loss가 없는 실험 중 일부가 loss가 상당히 높고 validation score가 낮기 때문이다. 이에 대한 이유가 모델이 canonical plane중 하나를 예측하지 않고 45도 미만의 각도를 가진 plane을 가지고 있음을 관찰하였다.
- Table을 보면 논문에서 제시한 모델이 sota임을 확인할 수 있다.

5. Conclusion
In this work, we introduced Dynamic Plane Convolutional Occupancy Networks, a novel implicit representation method for 3D reconstruction from point clouds. We proposed to learn dynamic planes to form informative features. We observe that 3 canonical planes are always predicted, and the symmetric property of objects are implicitly encoded. We also find that enforcing a similarity loss on the predicted plane normals considerably improves the performance on unseen object poses. In future work, we plan to assess the theoretical support for the dynamic plane prediction.
- 논문에서는 3D reconstruction을 위한 새로운 implicit representation인 Dynamic Plane Convolutional Occupancy Networks를 소개했다. 여기서는 유익한 feature를 학십하기 위해 dynamic plane을 학습할 것을 제안했다. 그리고 3개의 canonical plane이 항상 예측되고 object의 symmetric한 속성이 implicit하게 encoding 됨을 관찰했다. 또한, similarity loss를 적용하면 보이지 않는 object pose에서 성능이 상당히 향상된다는 것도 발견했다.
- 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.
Uploaded by N2T
'Paper Summary' 카테고리의 다른 글
| GanHand: Predicting Human Grasp Affordances in Multi-Object Scenes, CVPR’19 (0) | 2023.04.06 |
|---|---|
| Convolutional Occupancy Networks, ECCV’20 (0) | 2023.03.26 |
| Occupancy Networks: Learning 3D Reconstruction in Function Space, CVPR’19 (1) | 2023.03.26 |
| Deep Marching Cubes: Learning Explicit Surface Representations, CVPR’18 (0) | 2023.03.26 |
| Generative Adversarial Networks, NIPS’14 (0) | 2023.03.26 |
