Hand-Object Contact Consistency Reasoning for Human Grasps Generation, ICCV’21

논문 링크 : https://openaccess.thecvf.com/content/ICCV2021/papers/Jiang_Hand-Object_Contact_Consistency_Reasoning_for_Human_Grasps_Generation_ICCV_2021_paper.pdf

1. Introduction

In this paper, we study the interactions via generation: As shown in Fig. 1, given only a 3D object in the world coordinate, we generate the 3D human hand for grasping it. We argue that it is critical for the hand contact points and object contact regions to reach mutual agreement and consistency for grasp generation. To achieve this, we propose to unify two separate models for both the hand grasp synthesis and object contact map estimation. We show that the consistency constraint between hand contact points and object contact map is not only useful for optimizing better grasps during training time by designing new losses, but also provides a self-supervised task to adjust the grasp when testing on a novel object.

• 본 논문에서는 generation을 통한 interaction을 연구한다. Fig. 1 과 같이 world 좌표계에 3D object만 주어졌을 때 이를 잡기 위한 3차원 사람 손을 생성한다. 저자는 손의 contact point, 물체의 contact region이 grasp 생성을 위해 일관성과 손-물체가 잘 상호작용할 수 있도록 하는 것이 중요하다고 주장한다. 이를 위해, 논문에서는 hand grasp synthesis을 위한 모델과 object contact map을 위한 모델을 통합하는 것을 제안하였다. 이는 손의 접촉 지점과 물체의 접촉 면적 사이의 일관성 제약이 새로운 손실을 새로운 loss를 만들어 학습 동안 더 좋은 grasp를 최적화시킬 뿐만 아니라, 테스트 시 새로운 물체에 대한 grasp를 조정하기 위해 self-supervised task을 제공한다는 것을 보여준다.

2가지의 모델

First, we train a Conditional Variational AutoEncoder [44] (CVAE) based network which takes the 3D object point clouds as inputs and predicts the hand grasp parameterized by a MANO model [41], namely GraspCVAE. During training the GraspCVAE, we design two novel losses with one encouraging the hand to touch the object surface and another forcing the object contact regions touched by the ground truth hand close to the predicted hand. With these two consistent losses, we observe more realistic and physically plausible grasps.

• 먼저 GraspCVAE를 학습하는데, 이는 3D object point cloud를 input으로 하고 MANO model에 의해 파라미터화 된 hand grasp를 예측하는 Conditional Variational AutoEncoder 기반의 네트워크이다. GraspCVAE를 학습하는 동안 새로운 2가지의 loss를 디자인하는데, 하나는 손이 물체 표현에 닿도록 유도하는 것이고 다른 하나는 GT hand가 만지는 object contact region을 예측된 손에 가깝게한다.(즉, 하나는 손 자체가 물체의 표면에 가깝게, 하나는 손이 물체와 접촉하는 부분을 특정지어줌) 이 두개의 loss를 통해, 더 real하고 그럴듯한 grasp를 관찰한다.

Second, given the hand grasp pose and object point clouds as inputs, we train another network that predicts the contact map on the object. We name this model the ContactNet. The key role of the ContactNet is to provide supervision to finetune GraspCVAE during test time when no ground truth is available. We design a self-supervised consistency task, which requires the hand contact points produced by the GraspCVAE to be consistent and overlapped with the object contact map predicted by the ContactNet. We use this self-supervised task to perform test-time adaptation which finetunes the GraspCVAE to generate a better human grasp.

• 둘째, hand grasp pose와 object point cloud가 input으로 주어지면, 물체애 대한 contact map을 예측하는 다른 네트워크를 학습하는 것이다. 이 모델의 이름은 ContactNet이다. ContactNet의 핵심은 GT를 사용하지 못할 때 테스트 동안 GraspCVAE를 finetune하기 위한 supervision을 제공하는 것이다. 저자는 GraspCVAE에 의해 생성된 hand contact point가 ContactNet에 의해 예측된 object contact map과 일치하고 중첩되어야 하는 self-supervised consistency task를 디자인한다. 이를 통해 GraspCVAE를 더 finetuning하여 더 나은 grasp를 생성한다.

• 실험은 Obman, HO-3D, FPHA를 포함한 여러 dataset에 실행하였다. 테스트 시간 동안 self-supervised task으로 최적화함으로써 unseen, out-of-domain object에 맞게 모델을 generalize하고 조정하여 큰 성능 향상을 이끌어냈다.

Contribution

1. human grasp generation의 학습을 위한 새로운 손-물체 접촉 일관성 제약

2. 테스트 시간 중에도 생성 모델을 조정할 수 있는 일관성 제약에 기반한 새로운 self-supervision task

3. in-domain 및 out-of-domain에서의 object 모두에 있어 grasp generation의 성능 향상

3. Approach

Our goal is generating hand meshes as human grasps given object point clouds as inputs. To deal with this problem, we utilize both hands and object contact information and make sure they are consistent with each other, as summarized in Fig. 2.

Training Stage.

In this stage, the inputs of GraspCVAE are both of hand and object, and GraspCVAE learns to synthesizing grasps in the hand reconstruction paradigm, where both of the its encoder and decoder will be used. Note that this follows the standard procedure in Conditional Variational Auto-Encoder (CVAE) [44].

• 학습 단계에서 GraspCVAE의 input은 hand, object 둘 다 이며, GraspCVAE는 encoder와 decoder가 모두 사용되는 hand reconstruction 과정에서 grasp를 합성하는 방법을 학습한다. 이는 CVAE의 일반적인 절차를 따른다.

Testing Stage.

Given a test object, we first generate an initial grasp from the GraspCVAE decoder (without the encoder). Then, the generated grasp is forwarded together with the object to the ContactNet to predict a target contact map. Since ContactNet is trained with ground truth data, where penetration between hand-object does not exist and hand fingers are touching the object surface closely, it will model the pattern of the ideal hand-object contact. We use the predicted contact map from the ContactNet as a target for finetuning and optimizing the grasps generated by GraspCVAE. If the grasp is predicted correctly from GraspCVAE, the object contact region from the predicted grasp should be consistent with the target object contact map. We use this consistency as a self-supervision signal to adapt grasps generated by GraspCVAE during test-time.

• Test object가 주어지면, 먼저 GraspCVAE의 decoder에서 initial grasp를 생성한다. 이렇게 생성된 grasp를 object와 함께 ContactNet으로 전달하여 target contact map을 예측한다. ContactNet은 hand-object 사이의 penetration이 존재하지 않고 손가락이 물체 표면에 가깝게 터치하는 GT data로 학습되기 때문에 이상적으로 hand-object contact pattern을 모델링한다. 논문에서는 GraspCVAE에 의해 생성된 grasp를 미세 조정하고 최적화하기 위해 ContactNet으로부터의 예측된 contact map을 사용한다. GraspCVAE에서 grasp를 올바르게 예측한 경우에, 예측된 grasp가 접촉하는 물체의 영역이 target object contact map과 일치해야한다. 이 일관성을 self-supervision signal로 사용하여 GraspCVAE에 의해 생성된 grasp를 조정한다.

3.1. Learning GraspCVAE

Usage and architecture

The GraspCVAE is a Conditional Variational Auto-Encoder (CVAE) [44] based generative network, which uses conditional information to control generation. For GraspCVAE, the conditional information is the object. In training, both of encoder and decoder of GraspCVAE is used to learn the grasp generation task in a hand reconstruction manner by taking in both of hand-object as input. At test-time, only its decoder is used to generate human grasp of a object with only the 3D object as the input (without using the grasp for input).

• GraspCVAE는 conditional information을 사용하여 생성을 제어하는 CVAE 기반 generative network이다. 이때, conditional information은 object이다. 학습에서 GraspCVAE의 encoder와 decoder는 hand-object를 input으로 받아 hand reconstruction 방식으로 grasp generation task를 학습하는데 사용된다. 테스트시에는 decoder만이 3D object를 input으로 사용하여 (input으로 grasp를 사용하지 않음) object에 대한 human grasp를 생성한다.

During training.

Given two point clouds of the hand $\mathcal{P}^h \in \mathbb{R}^{778 \times 3}$ and the object $\mathcal{P}^o \in \mathbb{R}^{N \times 3}$ (where N is the number of points) as inputs, we use two separate PointNets [38] to extract their features respectively, denoted as $\mathcal{F}^h, \mathcal{F}^o \in \mathbb{R}^{1024}$. These two features are then concatenated as $\mathcal{F}^{ho}$ for the GraspCVAE encoder inputs. The outputs of the encoder are the mean $\mu \in \mathbb{R}^{64}$ and variance $\sigma^2 \in \mathbb{R}^{64}$ of the posterior Gaussian distribution $Q(z|\mu,\sigma^2)$ [27]. To reconstruct the hand, we first sample a latent code z from the distribution and the posterior distribution ensures the sampled latent code z is in correspondence with the input hand-object.

• Hand point cloud $\mathcal{P}^h \in \mathbb{R}^{778 \times 3}$, object point cloud $\mathcal{P}^o \in \mathbb{R}^{N \times 3}$ (여기서 N은 point의 개수) 이 input으로 주어지면, 각각 PointNet을 통해 $\mathcal{F}^h, \mathcal{F}^o \in \mathbb{R}^{1024}$ 라는 feature를 뽑는다. 이 두 feature는 $\mathcal{F}^{ho}$ 로 concat되어져 GraspCVAE encoder의 input이 된다. Encdoer의 output은 posterior Gaussian distribution $Q(z|\mu,\sigma^2)$ 의 평균 $\mu \in \mathbb{R}^{64}$ 과 분산 $\sigma^2 \in \mathbb{R}^{64}$ 이다. Hand reconstruction을 위해 먼저 distribution에서 latent code z를 sampling하고, posterior distribution은 sampling된 latent code z가 input hand-object와 일치하는지 확인한다.

The decoder takes the concatenation of latent code z and the object feature $\mathcal{F}^o$ as input to reconstruct a hand mesh, which is represented by a differentiable MANO model [41]. The MANO model is parameterized by the shape parameter $\beta \in \mathbb{R}^{10}$ for person-specific hand shape, as well as the pose parameter $\theta \in \mathbb{R}^{51}$ for the joint axis-angles rotation and root joint translation. Given the predicted parameters $(\hat\beta, \hat\theta)$ from the decoder, the MANO model forms a differentiable layer which outputs the shape of the hand with $\mathcal{\hat{M}} = (\mathcal{\hat{V}} \in \mathcal{R}^{778 \times 3}, \hat{F})$, where $\mathcal{\hat{V}}$, $\hat{F}$ denotes the mesh vertices and faces.

• Decoder는 differentiable MANO model로 표현되는 hand mesh를 reconstruction하기 위해 latent code z와 object feature $\mathcal{F}^o$ 의 concatenation을 input으로 받는다. MANO model은 특정 사람의 hand shape을 위해 shape parameter $\beta \in \mathbb{R}^{10}$ 와 joint axis-angle rotation과 root joint traslation을 표현하기 위해 pose parameter $\theta \in \mathbb{R}^{51}$ 로 매개변수화 되어있다. 예측된 파라미터 $(\hat\beta, \hat\theta)$ 가 decoder로 부터 주어지면, MANO model은 hand shape $\mathcal{\hat{M}} = (\mathcal{\hat{V}} \in \mathcal{R}^{778 \times 3}, \hat{F})$ 을 출력하는 differentiable layer를 형성한다. 여기서, $\mathcal{\hat{V}}$, $\hat{F}$ 는 각각 mesh의 vertex와 face이다.

During testing.

We only utilize the decoder from the GraspCVAE for inference. Given only the extracted object point cloud feature $\mathcal{F}^o$ and a latent code z randomly sampled from a Gaussian distribution as inputs, the decoder will generate the parameters for the MANO model which leads to the hand mesh output.

• Inference를 위해서는, GraspCVAE의 decoder만을 사용한다. 추출된 object point cloud feature $\mathcal{F}^o$ 와 Gaussian distribution에서 random하게 샘플링된 latent code z가 input으로 주어지면, decoder는 MANO parameter를 생성하게 된다.

Baseline

The first objective for the baseline model is mesh reconstruction error, which is defined on both the vertices of the mesh as well as the parameters of the MANO model. We adopt the $L_2$ distance to compute the error. We denote the reconstruction loss between the predicted vertices and the ground-truths as $L_{\mathcal{V}} = || \hat{\mathcal{V}} - \mathcal{P}^h||^2_2$. The losses on MANO parameters are defined in a similar way with $L_\theta$ and $L_\beta$. The reconstruction error can be represented as $L_{\mathcal{R}} = \lambda_\mathcal{V} \cdot L_\mathcal{V} + \lambda_\theta \cdot L_\theta + \lambda_\beta \cdot L_\beta$, where $\lambda_{\mathcal{V}}$, $\lambda_\theta$ and $\lambda_\beta$ are constants balancing the losses.

• Baseline model의 첫 번째 목표는 mesh reconstruction error이며, 이는 mesh의 vertex와 MANO model의 매개변수 모두에서 정의된다. 오차를 계산하기 위해 $L_2$ loss를 사용한다. 예측된 vertex와 GT 사이의 reconstruction loss는 $L_{\mathcal{V}} = || \hat{\mathcal{V}} - \mathcal{P}^h||^2_2$ 이다. MANO parameter의 loss는 비슷한 방식으로 $L_\theta$ 와 $L_\beta$ 로 정의된다. Reconstruction error는 이 3가지의 Loss에 각각 weight term을 붙여 합한것과 같다.

Following the training of VAE [27], we define a loss enforcing the latent code distribution $Q(z|\mu,\sigma^2)$ to be close to a standard Gaussian distribution, which is achieved by maximizing the KL-Divergence as $L_{\mathcal{KLD}} = -KL(Q(z|\mu,\sigma^2)||\mathcal{N}(0,I))$. We also encourage the grasp to be physically plausible, which means the object and hand should not penetrate into each other. We denote the object point subset that is inside the hand as $\mathcal{P}^o_{in}$, then the penetration loss is defined as minimizing their distances to their closest hand vertices $L_{penetr} = \frac{1}{|\mathcal{P}^o_{in}|} \sum_{p \in \mathcal{P}^o_{in}} min_i||p-\hat{V}_i||^2_2$. In a short summary, the loss for training the baseline is:

where $\lambda_{\mathcal{KLD}}$ and $\lambda_p$ are constants balancing the losses.

• VAE의 학습방법처럼, latent code distribution $Q(z|\mu,\sigma^2)$ 을 standard Gaussian distribution과 가깝게 하기위해 loss를 정의하는데, 이는 KL-Divergence($L_{\mathcal{KLD}} = -KL(Q(z|\mu,\sigma^2)||\mathcal{N}(0,I))$)를 최대화 시키는 것이다. 그리고 object와 hand가 각각 penetration이 없게끔 장려하는 loss도 사용한다. 이는 hand 안에 들어가있는 object point subset을 $\mathcal{P}^o_{in}$ 라고 하였을때, penetration loss($L_{penetr} = \frac{1}{|\mathcal{P}^o_{in}|} \sum_{p \in \mathcal{P}^o_{in}} min_i||p-\hat{V}_i||^2_2$)는 각 object point와 가장 가까운 vertex와의 거리를 최소화 시키도록 하는 loss이다. Baseline을 학습하기 위한 loss는 다음과 같다.

Reasoning Contact in Training

There are two potential challenges in the baseline framework: First, the losses in the baseline model ignore physical contact between the hand-object, which cannot ensure the stability of the grasp; Second, grasp generation is multi-modal and the ground-truth hand pose is not the only answer. To tackle these challenges, we design two novel losses from both the hand and the object aspects to reason plausible hand-object contact and find the mutual agreement between them.

• 기본 framework에는 두 가지 잠재적인 문제가 있다. 첫째, 베이스라인 모델의 손실은 hand-object 간의 물리적인 접촉을 무시하므로 grasp의 안정성을 보장할 수 없다. 둘째, grasp generation은 multi-modal 이며 GT hand pose가 유일한 정답은 아니다. 이러한 문제를 해결하기 위해 그럴듯한 손-물체 접촉을 추론하고 이들 사이의 상호 일치를 찾기 위해 손과 물체 측면에서 두 가지 새로운 손실을 설계한다.

Object-centric Loss.

From the object perspective, there are regions that are often contacted by human hand. We encourage the human hand to get close to these regions using the object-centric loss. Specifically, from the ground-truth hand-object interaction, we can derive the object contact map $\Omega \in \mathbb{R}^{N}$ by normalizing the distance $\mathbf{D}(\mathcal{P}^o)$ between all object points and their nearest hand prior vertices with function f(·), where $f(\mathbf{D}(\mathcal{P}^o)) = 1-2 \cdot(Sigmoid(2\mathbf{D}(\mathcal{P}^o))-0.5)$. The distances are in centermeter and contact map scores are in [0, 1]. Then we force the object contact map $\hat{\Omega}$ computed from the generated hand to be close to the ground truth $\Omega$, using loss

• Object 측면에서 human hand에 의해 종종 contact 되는 region이 있다. 저자는 human hand가 이 region에 가깝게 하기 위해 object-centric loss를 사용한다. 구체적으로, 모든 object point와 그에 가장 가까운 hand prior vertex 사이의 거리 $\mathbf{D}(\mathcal{P}^o)$ 를 normalizing 함으로써, GT hand-object interaction으로 부터 object contact map $\Omega \in \mathbb{R}^{N}$ 을 얻을 수 있다. $f(\mathbf{D}(\mathcal{P}^o)) = 1-2 \cdot(Sigmoid(2\mathbf{D}(\mathcal{P}^o))-0.5)$ 이 식을 통해 각 object point에 대해 [0,1]의 value를 가지는 contact map을 얻을 수 있다. 그런 다음 loss를 사용하여 생성된 손에서 계산된 object contact map이 GT $\Omega$ 와 가까워 지도록 한다.

Hand-centric Loss.

We define the prior hand contact vertices $\mathcal{V}^p$ as shown in Fig. 5, motivated by [20, 2]. Given the predicted locations of the hand contact vertices, we then take the object points nearby as possible points to contact. Specifically, for each object point $\mathcal{P}^o_i$, we compute the distance $\mathbf{D}(\mathcal{P}_i^o) = min_j||\mathcal{V}_j^p - \mathcal{P}_i^o||^2_2$, and if it is smaller than a threshold, we take it as the possible contact point on the object. Our hand-centric objective is to push the hand contact vertices close to the object as,

for all the possible contact points on the object, where $\mathcal{T}$ = 1 cm is the threshold. The final loss combining the two novel losses above is,

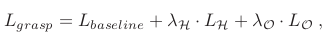
where $\lambda_ \mathcal{H}$ and $\lambda_ \mathcal{O}$ are constants balancing the losses.

• 논문에서는 prior hand contact vertex를 $\mathcal{V}^p$ 로 정의하였다. hand contact vertices의 예측된 위치가 주어지면 접촉 가능한 지점 근처의 object point를 취한다. 구체적으로, 각 object point $\mathcal{P}^o_i$에 대해 $\mathbf{D}(\mathcal{P}_i^o) = min_j||\mathcal{V}_j^p - \mathcal{P}_i^o||^2_2$ 라는 거리를 계산하는데, threshold보다 작으면 이를 물체에 대해 가능한 contact point로 받아들인다. Hand-centric의 목표는 물체에 가능한 모든 접점에 대해 hand contact vertex가 object에 가까워지게 하는 것이다. 여기서 threshold를 1cm로 두었다. 최종 loss는 baseline loss에 위의 두 Loss를 결합한 형태가 된다.

Intuitively, the $L_{\mathcal{O}}$ generally answers the question Where to grasp? and does not specify which hand part should be close to the object contact regions. And $L_{\mathcal{H}}$ is used to find the answer of Which finger should contact? During training, with the two proposed losses, the hand contact points and object contact region will reach mutual agreement and be consistent to each other for generating stable grasps.

• 직관적으로, $L_{\mathcal{O}}$ 는 어디를 잡아야 하는가?에 대해 일반적인 대답이 된다. 하지만, 손의 어떤 부분이 object contact region에 가까워야 하는지를 지정하지는 않는다. 그리고 $L_{\mathcal{H}}$ 는 어떤 손가락이 접촉되어야 하는가? 에 대한 정답을 찾기위해 사용된다. 학습동안 위에서 제시된 두 loss로 hand contact point와 object contact region이 상호간 합의에 도달하고, 서로 일관되게 유지되어 안정적인 grasp를 생성할 수 있다.

3.2. Learning ContactNet

We propose another network, the ContactNet, to model the contact information between the hand-object as shown in Fig. 6. The inputs are hand and object point cloud, and the output is the object contact map denoted as $\Omega^c \in \mathbb{R}^N$ for $N$ object points. We use two PointNet encoders to extract hand and object feature maps. Since we need to predict the contact score for each point ($\Omega^c_i$ should be the score for $\mathcal{P}^o_i$), we utilize the per-point object local feature $\mathcal{F}^s \in \mathbb{R}^{N \times 64}$ of the PointNet encoder to ensure this correspondence. We also make use of hand and object global feature by first summing them then duplicate N times and concatenate it with the object local feature for a to dimension $\mathbb{R}^{N \times 1024}$ feature maps. Given these features, we apply four layers of 1-D convolution on top to regress the object contact map activated by the sigmoid function. The loss for training is the $L_2$ distance between the predicted contact map $\Omega^c$ and ground-truth $\Omega$ as, $L_{cont} = ||\Omega^c - \Omega||^2_2$.

• 다음은, Fig. 6과 같이 hand-object 간의 contact 정보를 모델링하기 위한 ContactNet에 대해 제안한다. Input은 hand, object point cloud이고, output은 object contact map이다. 논문에서는 두 개의 PointNet encoder를 사용하여 hand, object feature map을 추출한다. 각 point에 대한 contact score를 예측해야하기 때문에, point 별 object local feature를 활용한다. 또한, hand와 object의 global feature도 사용한다. 이를 4개의 1-D convolution layer를 적용하여 object contact map을 regression하는 작업을 하게된다. 학습 시에 손실로는 $L_2$ distance를 사용하여, 예측된 contact map과 GT contact map을 비교하게된다.

3.3. Contact Reasoning for Test-Time Adaption

During testing, we unify the GraspCVAE and ContactNet in a cascade manner as shown on the right side of Fig. 2. Given the object point clouds as inputs, the GraspCVAE will first generate a hand mesh $\hat{\mathcal{M}}$ as the initial grasp. We compute its object contact map $\Omega_{\hat{\mathcal{M}}}$ correspondingly. Taking both the predicted hand mesh and object as inputs, the ContactNet will predict another contact map $\Omega^c$. If the grasp is predicted correctly, the two contact map $\Omega_{\hat{\mathcal{M}}}$ and $\Omega^c$ should be consistent. Based on this observation, we define a self-supervised consistency loss as $L_{refine} = ||\Omega_{\hat{\mathcal{M}}} - \Omega||^2_2$ for fine-tuning the GraspCVAE. Besides this consistency loss, we also incorporate the hand-centric loss $L_{\mathcal{H}}$ and penetration loss $L_{penetr}$ to ensure the grasp is physically plausible. We apply the joint optimization with all three losses on a single test example as,

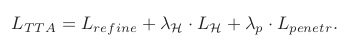
We use this loss to update the GraspCVAE decoder, and freeze other parts of the two networks.

• 테스트 동안은 Fig 2.의 오른쪽과 같이 GraspCVAE와 ContactNet을 계단식으로 통합한다. Object point cloud가 input으로 주어지면 GraspCVAE는 먼저 initial grasp로 hand mesh를 생성한다. 이에 따라 object contact map($\Omega_{\hat{\mathcal{M}}}$)을 계산한다. 예측된 hand mesh와 object를 모두 input으로 사용하여 ContactNet은 다른 contact map ($\Omega^c$)을 예측한다. 올바른 grasp가 예측되면, 두 contact map이 일치해야한다. 이 prior를 기반으로 GraspCVAE를 fine-tuning하기 위해 self-supervised consistency loss를 $L_2$ loss를 사용하여 정의한다. 이 일관성 손실 이외에도 hand-centric, penetration loss를 통합하여 grasp가 그럴듯하게 한다. 이의 3가지 loss를 이용해 테스트 예제에서 최적화를 적용한다. (TTA = test-time adaptation) 이 loss는 GraspCVAE의 decoder를 업데이트하는데에만 사용된다.

4. Experiment

4.2. Datasets

Obman Dataset

train set

HO-3D and FPHA Dataset

test set (object가 12종류밖에 없음)

4.3. Evaluation Metrics

Penetration → depth, volume (low)

Grasp displacement → mean, variance (grasp의 stability measure) (low)

Perceptual score → 자연스러움 평가 (high)

Hand-object contact metrics → 손-물체 접촉 비율, 개별 물체와 손 접촉 비율, 물체에 접촉하는 손가락의 수를 계산. (high)

4.4. Grasp Generation Performance

Qualitative results.

• 위는 in-domain(Obman), 아래는 out-of-domain(HO-3D) 이다.

Quantitative results.

• 기존 SOTA보다 성능이 월등히 좋음

4.5. Ablation Study

4.5.1 GraspCVAE Training Objectives

• $\mathcal{L}_\mathcal{H}, \mathcal{L}_\mathcal{O}$ 의 효과에 대한 추가적인 연구이다. $\mathcal{L}_\mathcal{H}$(gt) 는 손가락이 dynamic하게 contact region을 찾는 것이 아닌 ground truth contact region을 터치하도록 강제하는건데, 성능이 더 낮아짐을 볼 수 있다. 그리고, $\mathcal{L}_\mathcal{O}$(dist) 는 GT hand-object distance와 예측된 hand-object distance간의 직접적인 잔차를 최소화 시키는데, 이는 contact map의 유효함을 실험하기 위함이다. 실제로 $\mathcal{L}_\mathcal{O}$(dist)를 사용했을 때 성능이 낮아졌다.

4.5.2. ContactNet Designs

• ContactNet의 input의 종류를 바꿔가면서 실험.

4.5.3 Test-Time Adaptation (TTA) for Generalization

TTA (offline)

• 학습 기반의 TTA, 각 sample에 적용되기 전에 network의 매개변수가 재초기화됨 (3.3 에서 제시한 방법)

TTA-optm (offline)

• 최적화 기반의 TTA, MANO parameter를 직접적으로 최적화시킴

TTA-noise (offline)

• 학습 기반의 TTA, ContactNet을 학습할 때 hand parameter에 random noise를 줌.

TTA-online

• 학습 기반의 TTA, 네트워크 매개변수는 각 비디오 시퀀스에 대해 한 번만 다시 초기화된다.

일반적으로 TTA를 사용한 부분이 성능이 더 좋음. 이에 대한 qualitative results는 아래와 같음.

• Fig 8 : penetration이 감소하였고, 손가락이 물체 표면에 더 가까워짐

• Fig 9 : object contact region이 더 넓어졌는데, 이는 grasp가 더 stable함을 이야기한다.

5. Conclusion

In this work, we propose a framework for generating human grasps given an object. To get natural and stable grasps, We reason the consistency of contact information between object and generated hand from two aspects: First, we design two novel training targets from the view of hand and object respectively, which helps them to find a mutual agreement on the form of contact. Second, we design two networks for grasp generation and predicting contact map respectively. We leverage the consistency between outputs of the two networks for designing a self-supervised task, which can be used at test-time for adapting generated grasps on novel objects.

• 논문에서는 object가 주어졌을 때 human grasp를 생성하기 위한 framework를 제안하였다. 자연스럽고 안정적인 grasp 생성을 위해 object와 생성된 손 사이의 접촉 정보의 일관성을 두 가지 측면에서 추론한다. 1) 손과 물체의 관점에서 각각 두 개의 새로운 학습 대상을 설계하여 접촉 형태에 대해 상호 합의점을 찾는다. 2) Grasp 생성 및 contact map 예측을 위한 두 개의 네트워크(GraspCVAE, ContactNet)를 각각 설계한다.

• 또한, self-supervision을 위해 두 network output간의 일관성을 이용하며, 이는 새로운 object에 대해 생성된 grasp를 적용하기 위해 test 시에 사용할 수 있다.

• 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.

Uploaded by N2T