SampleNet: Differentiable Point Cloud Sampling, CVPR’20

 

논문 링크 : https://openaccess.thecvf.com/content_CVPR_2020/papers/Lang_SampleNet_Differentiable_Point_Cloud_Sampling_CVPR_2020_paper.pdf

Abstract

Classic sampling approaches, such as farthest point sampling (FPS), do not consider the downstream task. A recent work showed that learning a task-specific sampling can improve results significantly. However, the proposed technique did not deal with the non-differentiability of the sampling operation and offered a workaround instead. We introduce a novel differentiable relaxation for point cloud sampling that approximates sampled points as a mixture of points in the primary input cloud. We also show that the proposed sampling method can be used as a front to a point cloud registration network.w

• Classic sampling 방법인 farthest point sampling은 downstream task를 고려하지 않는다. 최근 연구에 따르면 task-specific sampling을 학습하면 결과가 크게 향상될 수 있다. 그러나 이는 미분 불가능성에 대해 다루지는 않는다. 저자는 novel differentiable point cloud sampling 방법을 소개하는데 이는 sampled point를 input point들의 혼합으로 근사한다. 또한 제안하는 샘플링 방법이 point cloud registration network의 앞단으로 사용될 수 있음을 보인다.

 

1. Introduction

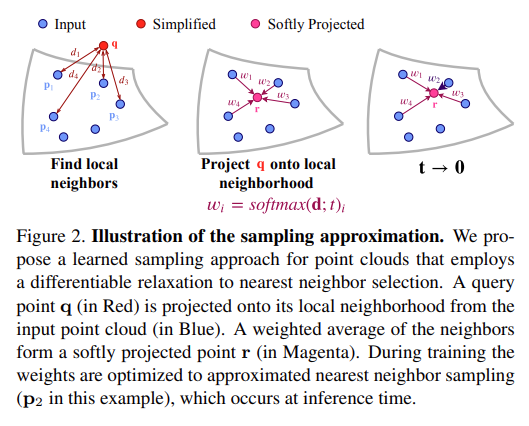
This learned sampling approach improved application performance with sampled point clouds, in comparison to non-learned methods, such as FPS and random sampling. However, the matching step is a non-differentiable operation and can not propagate gradients through a neural network. We extend the work of Dovrat et al. [6] by introducing a differentiable relaxation to the matching step, i.e., nearest neighbor selection, during training (Figure 2). This operation, which we call soft projection, replaces each point in the simplified set with a weighted average of its nearest neighbors from the input.

• 본 논문에서 제시하는 학습된 sampling approach는 FPS 및 random sampling과 같은 비학습 방법과 비교하여 sampling된 point cloud로 application 성능을 개선했다. 그러나 matching step은 non-differentiable operation이며 neural network를 통해 gradient의 전파가 불가능하다. 저자는 학습 도중에 nearest neighbor selection에 differentiable relaxation을 도입함으로써 이 전 논문의 work를 확장한다. 이러한 연산을 soft projection 이라고 하는데, 이는 단순화된(input 보다 작은 point set 크기를 얘기함.) set의 각 point를 input에 대한 nearest neighbor의 weighted sum으로 바꾼다.

During training, the weights are optimized to approximate the nearest neighbor selection, which is done at inference time. The soft projection operation makes a change in representation. Instead of absolute coordinates in the free space, the projected points are represented in weight coordinates of their local neighborhood in the initial point cloud.

• 학습동안 weight는 inference 동안 nearest neighbor selection에 근사하도록 최적화 된다. Soft projection operation은 representation을 변경한다. Free space에서 absolute coordinate 대신, projected point는 initial point cloud에서 local neighborhood의 weight coordinate로 표시된다.

 

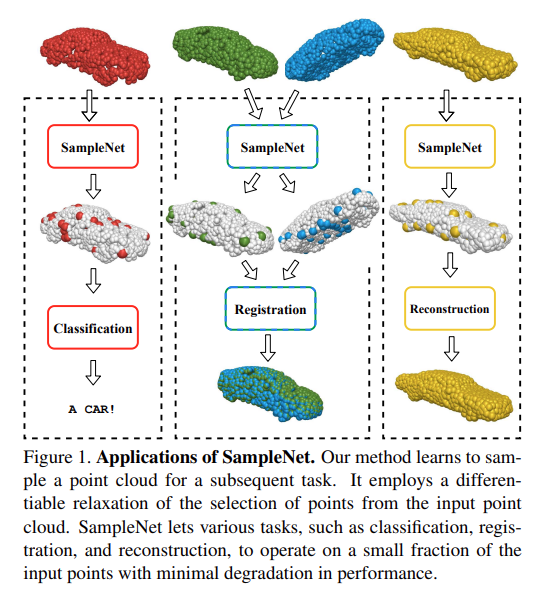
Our method, termed SampleNet, is applied to a variety of tasks, as demonstrated in Figure 1. Extensive experiments show that we outperform the work of Dovrat et al. consistently. Additionally, we examine a new application registration with sampled point clouds and show the advantage of our method for this application as well. Registration introduces a new challenge: the sampling algorithm is required to sample consistent points across two different point clouds for a common downstream task. To summarize, our key contributions are threefold:

• SampleNet이라고 불리는 제시된 method는, Fig. 1과 같이 다양한 task에 적용된다. 광범위한 실험이 이전 Learning to Sample 논문의 성능을 능가한다는 것을 보여준다. 또한 sampled point cloud를 사용하여 새로운 application인 registration을 실험하고 이 application에 대한 방법의 이점도 보여준다. Registration에서는 새로운 문제가 발생하는데, 공통 downstream 작업에 대해 두 개의 서로 다른 point cloud에서 일관된 point를 샘플링하려면 sampling algorithm이 필요하다.

Contribution

A novel differentiable approximation of point cloud sampling.

• Point cloud sampling에 대한 novel differentiable approximation

Improved performance with sampled point clouds for classification and reconstruction tasks, in comparison to non-learned and learned sampling alternatives.

• 비학습 및 미리 학습된 샘플링 방법과 비교하여 reconstruction과 classification task에서 sampling된 point cloud로 성능 향상을 이루었음.

Employment of our method for point cloud registration.

• 이 방법을 point cloud registration에 사용하였음.

 

3. Method

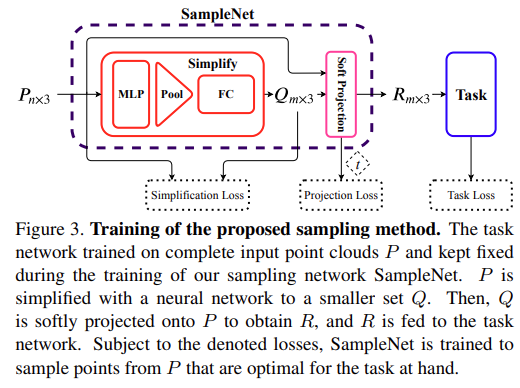
An overview of our sampling method, SampleNet, is depicted in Figure 3. First, a task network is pre-trained on complete point clouds of n points and frozen. Then, SampleNet takes a complete input P and simplifies it via a neural network to a smaller set Q of m points [6]. Q is soft projected onto P by a differentiable relaxation of nearest neighbor selection. Finally, the output of SampleNet, R, is fed to the task.

• 샘플링 방법인 SampleNet은 Fig. 3에 나와있다. 먼저 task network는 n개 point의 온전한 point cloud에서 pre-train되고 고정된다. 그런 다음 SampleNet은 온전한 input P를 받아서 neural network를 통해 m-point의 더 작은 set Q로 단순화 된다. Q는 nearest neighbor selection의 differentiable relaxation에 의해 soft project된다. 마지막으로 SampleNet R의 output이 task의 input이 된다.

loss

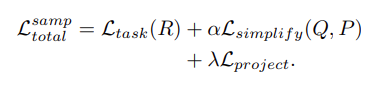
The first term,${\mathcal{L}}_{task}(R)$, optimizes the approximated sampled set$R$ to the task. It is meant to preserve the task performance with sampled point clouds.${\mathcal{L}}_{simplify}(Q,P)$ encourages the simplified set to be close to the input. That is, each point in$Q$ should have a close point in P and vice-versa. The last term,${\mathcal{L}}_{project}$ is used to approximate the sampling of points from the input point cloud by the soft projection operation.

• 첫 번째 term인 task loss는 approximate 된 sampled set R을 task에 최적화시킨다. 이는 샘플링된 point cloud로 task 성능을 유지하기 위한 것이다. Simplify loss는 단순화된 set을 input에 가깝게 하도록 한다. 즉, simplified된 set Q의 각 점은 input P에 가까운 점을 가지고 있어야 하며, 그 반대의 경우도 마찬가지이다. 마지막 항인 Projection loss는 soft projection operation에 의해 input point cloud에서 point sampling을 approximation 하는 데 사용된다.

 

3.1. Simplify

Given a point cloud of$n$ 3D coordinates$P\in {\mathbb{R}}^{n\times 3}$, the goal is to find a subset of m points$R^{\ast }\in {\mathbb{R}}^{m\times 3}$, such that the sampled point cloud$R^{\ast }$ is optimized to a task$T$. Denoting the objective function of$T$ as$\mathcal{F},R^{\ast }$ is given by:

• n 개의 3D coordinate가 있는 point cloud가 주어지면, 목표는 m point의 subset을 찾는 것이다. 이떄의 sampled point cloud subset은 task T에 optimize된 상태이다. 즉 식으로 표현하면 아래와 같다.

This optimization problem poses a challenge due to the non-differentiability of the sampling operation. In order to encourage the second property, a simplification loss is utilized. Denoting average nearest neighbor loss as:

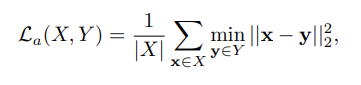
• 이 optimization 문제는 sampling operation의 non-differentiability로 인해 문제가 된다. 이를 위해 simplification loss가 사용된다. Average nearest neighbor loss는 다음과 같다.

• 아래는 maximal nearest neighbor loss이다.

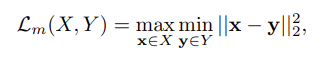
• 그리고 최종 simplification loss는 다음과 같다.

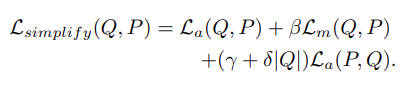
In order to optimize the point set Q to the task, the task loss is added to the optimization objective. The total loss of the simplification network is:

• Point set Q를 task에 optimize 시키기 위해, task loss를 추가하였다. 따라서 total loss는 다음과 같다.

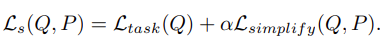
The simplification network described above is trained for a specific sample size m. This network orders the simplified points according to their importance for the task and can output any sample size. It outputs n points and trained with simplification loss on nested subsets of its output:

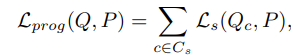
• 위에서 설명한 simplification network는 특정 샘플 크기 m에 대해 학습된다. 이 네트워크는 task의 중요도에 따라 단순화된 point를 주문하고 모든 sample size를 출력할 수 있다. 이는 n개의 point를 출력하고 output의 중첩된 subset에 대한 simplification loss로 학습된다.

 

3.2 Project

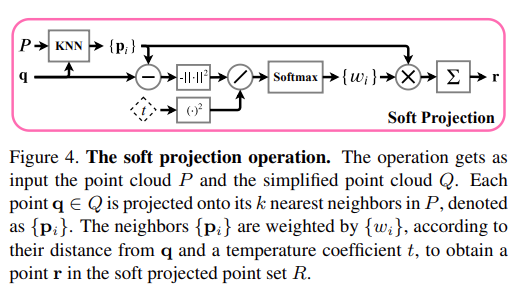
Instead of optimizing the simplified point cloud for the task, we add the soft projection operation. The operation is depicted in Figure 4. Each point q ∈ Q is softly projected onto its neighborhood, defined by its k nearest neighbors in the complete point cloud P, to obtain a projected point r ∈ R. The point r is a weighted average of original points form P:

• Task에 대해 단순화된 point cloud를 optimize하는 대신 soft projection operation을 추가한다. (Fig. 4) 각 점 q는 projected point r을 얻기 위해 complete point cloud P에서 knn으로 정의되는 neighbor에 soft projection된다. point r은 original point form P의 weighted averge이다.

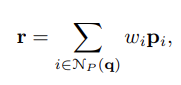
where${\mathcal{N}}_P(q)$ contains the indices of the k nearest neighbors of q in P. The weights$\{w_i\}$ are determined according to the distance between q and its neighbors, scaled by a learnable temperature coefficient t:

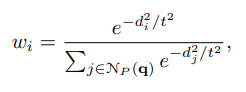
• ${\mathcal{N}}_P(q)$ 는 P에서 q의 knn에 대한 index를 포함하고 있다. Weight$\{w_i\}$ 는 학습 가능한 coefficient t에 의해 조정된 q와 neighbor 사이의 거리에 따라 결정된다. (여기서 distance는 q와 p_i 사이의 l2-norm)

The neighborhood size$k=|{\mathcal{N}}_P(q)|$ plays a role in the choice of sampled points. Through the distance terms, the network can adapt a simplified point’s location such that it will approach a different input point in its local region. While a small neighborhood size demotes exploration, choosing an excessive size may result in loss of local context.

• Neighborhood size$k=|{\mathcal{N}}_P(q)|$ 는 sampled point choice에 중요한 역할을 한다. Distance term을 통해 network는 local 영역의 다른 input point에 접근하도록 simplified point location을 조정할 수 있다. 작은 neighborhood size는 탐색 수준을 낮추지만, 과도한 크기를 선택하면 local context가 손실될 수 있다.

The weights$\{w_i\}$ can be viewed as a probability distribution function over the points$\{p_i\}$, where r is the expectation value. The temperature coefficient controls the shape of this distribution. In the limit of t → 0, the distribution converges to a Kronecker delta function, located at the nearest neighbor point.

• Weight$\{w_i\}$ 는$\{p_i\}$ 점에 대한 확률분포함수로 볼 수 있다. 여기서 r은 기대값이다. temperature coefficient는 이 distribution의 shape을 제어한다. t → 0의 한계에서 분포는 가장 가까운 이웃 점에 위치한 Kronecker delta function으로 수렴된다.

Given these observations, we would like the point r to approximate nearest neighbor sampling from the local neighborhood in P. To achieve this we add a projection loss, given by:

• 이러한 관찰이 주어지면 point r이 P의 local neighborhood에서 nearest neighbor sampling을 approximate되길 원한다. 이를 달성하기 위해 다음과 같이 projection loss를 추가한다.

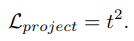
In our sampling approach, the task network is fed with the projected point set R rather than simplified set Q. Since each point in R estimates the selection of a point from P, our network is trained to sample the input point cloud rather than simplify it. Our sampling method can be easily extended to the progressive sampling settings (Equation 7). In this case, the loss function takes the form:

• 샘플링 접근 방식에서 task network에는 단순화된 집합 Q가 아닌 projection된 point set R이 제공된다. R의 각 포인트는 P에서 point selection을 추정하기 때문에 network는 input point cloud를 단순화시키기 보다는 sampling 하도록 학습되었다. 이 sampling 방법은 점진적 샘플링 설정으로 쉽게 확장할 수 있다. 이 경우 loss function은 다음과 같다.

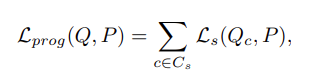
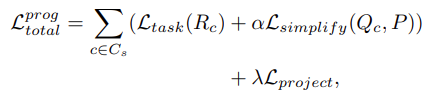
At inference time we replace the soft projection with sampling, to obtain a sampled point cloud$R^{\ast }$. Like in a classification problem, for each point$r^{\ast }\in R^{\ast }$, we select the point$p_i$ with the highest projection weight:

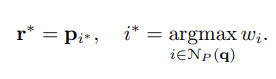
• Inference 시간에 저자는 soft projection을 sampling으로 대체하여 sampling된 point cloud$R^{\ast }$ 를 얻는다. Classification 문제와 같이 각 point$r^{\ast }$ 에 대해 projection weight이 높은 점$p_i$ 를 선택한다.

 

5. Conclusion

We presented a learned sampling approach for point clouds. Our network, SampleNet, takes an input point cloud and produces a smaller point cloud that is optimized to some downstream task. The key challenge was to deal with the non-differentiability of the sampling operation. To solve this problem, we proposed a differentiable relaxation, termed soft projection, that represents output points as a weighted average of points in the input.

• Point cloud에 대해 학습된 sampling approach 제시. SampleNet은 input point cloud를 가져와 일부 downstream 작업에 최적화된 더 작은 point cloud를 생성함. 주요 과제는 sampling 작업의 미분 불가능성을 처리하는 것임. 이 문제를 해결하기 위해 input에 있는 point의 weighted sum으로 output point를 나타내는 differentiable relaxation(soft projection)을 제안하였음.

During training, the projection weights were optimized to approximate nearest neighbor sampling, which occurs at the inference phase. The soft projection operation replaced the regression of optimal points in the ambient space with multiple classification problems in local neighborhoods of the input.

• 학습 동안 projection weight은 nearest neighbor sampling을 근사하도록 최적화되었다. Soft projection operation은 주변 공간의 optimal point regression을 input local neighborhood의 여러 classification 문제로 대체했다.

 

 

Uploaded by

N2T