논문 링크 : https://openaccess.thecvf.com/content/ICCV2021/papers/Lin_Mesh_Graphormer_ICCV_2021_paper.pdf
1. Introduction
Transformers are good at modeling long-range dependencies on the input tokens, but they are less efficient at capturing fine-grained local information.
Convolution layers, on the other hand, are useful for extracting local features, but many layers are required to capture global context.
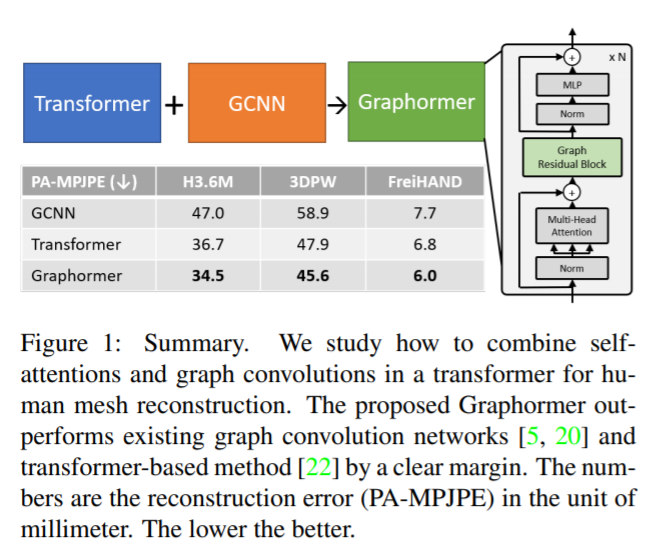
We present a graph-convolution-reinforced transformer called Mesh Graphformer for reconstructing human pose and mesh from a single image.
We inject graph convolutions into transformer blocks to improve the local interactions among neighboring vertices and joints.
In order to leverage the power of graph convolutions, Graphormer is free to attend to all image grid features that contain more detailed local information and are helpful in refining the 3D coordinate prediction.
- graph convolution 의 이점을 얻기위해, Graphormer 는 더 자세한 local information 을 포함하거나 3D coordinate prediction 을 개선하는데 도움이되는 모든 image grid feature 에 자유롭게 주의를 기울인다.
Consequently, Graphormer and image grid features are mutually reinforced to achieve better performance in human pose and mesh reconstruction.
Contribution
- We present a graph-convolution-reinforced transformer called Mesh Graphormer to model both local and global interactions for the 3D reconstruction of human pose and mesh.
- Mesh Graphormer allows joints and mesh vertices to freely attend to image grid features to refine the 3D coordinate prediction.
- Mesh Graphormer outperforms previous state-of-theart methods on Human3.6M, 3DPW, and FreiHAND datasets.
3. Graphormer Encoder

It consists of a stack of N = 4 identical blocks. Each block consists of five sub-modules, including a Layer Norm, a Multi-Head Self-Attention module, a Graph Residual Block, a second Layer Norm, and a Multi-Layer Perceptron (MLP) at the end.
We introduce graph convolution into the network to model fine-grained local interactions.
3.1 Multi-Head Self-Attention
We employ the Multi-Head Self-Attention (MHSA) module proposed by Vaswani et al. [35], which uses several self-attention functions in parallel to learn contextual representation.
Given an input sequence , where d is the hidden size.
It first projects the input sequence to queries Q, keys K, and values V by using trainable parameters . That is written as

The three feature representations are split into h different subspaces, e.g., where , so that we can perform self-attention for each subspace individually.
For each subspace, the output are computed by:

where Att(·) denotes the attention function [35] that quantifies how semantically relevant a query is to keys by scaled dot-product and softmax.
The output ∈ R n× d h from each subsapce are later concatenated to form the final output .
3.2 Graph Residual Block
MHSA 가 long-range dependencies 를 추출하는 데에 있어서 유용하지만, fine-grained local information 을 capture 하는 것은 덜 효율적이다. 이를 해결하기 위해 Graph Residual Block 을 소개한다.
Given the contextualized features generated by MHSA, we improve the local interactions with the help of graph convolution:

According to BERT [6], we use the Gaussian Error Linear Unit (GeLU) [11] in this work.
Our Graph Residual Block makes it possible to explicitly encode the graph structure within the network and thereby improve spatial locality in the features.
4. Graphormer for Mesh Reconstruction

An image with a size of 224x224 is used as input and image grid features are extracted. The image features are tokenized as input for a multi-layer Graphormer encoder. In the end, our end-to-end framework predicts 3D coordinates of the mesh vertices and body joints at the same time.
4.1 CNN and Image Grid Features
In the first part of our model, we use a pre-trained imagebased CNN for feature extraction.
- 이전 work 에서는 global 2048-Dim image feature vector를 model input 으로 추출하였는데 이는 fine-grained local details 를 포함하지 않는다는 단점이 있다.
This motivates us to add grid features [13] as input tokens and allow joints and mesh vertices to freely attend to all the grid features.
- 실험에서 보일 것 처럼, grid feature 에 의해 제공되는 local information 은 Graphormer 안에 graph convolution 에 의해 3D mesh position 과 body joint 를 개선하는 데에 효율적으로 이점이 있다.
As shown in Figure 3(a), we extract the grid features from the last convolution block in CNN. The grid features are typically 7 × 7 × 1024 in size. They are tokenized to 49 tokens, and each token is a 1024-Dim vector.
We also extract the 2048-Dim image feature vector from the last hidden layer of the CNN and perform positional encoding using the 3D coordinates of each vertex and body joint in a human template mesh.
Finally, we apply MLP to make the size of all input tokens consistent. After that, all input tokens have 2051-Dim.
4.2 Multi-Layer Graphormer Encoder
Given the grid features, joint queries, and vertex queries, our multi-layer Graphormer encoder sequentially reduces the dimensions to map the inputs to 3D body joints and mesh vertices at the same time.

The three encoder blocks have the same number of tokens including 49 grid feature tokens, 14 joint queries, and 431 vertex queries.
Our multi-layer Graphormer encoder processes a coarse mesh with 431 vertices.
We use a coarse template mesh for positional encoding, and our Graphormer encoder outputs a coarse mesh.
Then, we use a linear projection to sample the coarse mesh up to the original resolution (with 6K vertices in SMPL mesh topology).
Learning a coarse mesh followed by upsampling is helpful to avoid redundancies in the original mesh and makes training more efficient.
5. Experiments




5.3 Ablation Study
Effectiveness of Grid Features

Grid Features 를 사용하면 성능이 더 높아짐.
The next question one may ask is what feature maps are important for training a transformer encoder.

The results suggest that the feature pyramid is helpful for improving the performance of a transformer encoder.
Effectiveness of Adding Graph Convolution

The results show some interesting observations: (i) Adding a graph convolution to Encoder1 or Encoder2 does not improve performance. (ii) Adding the graph convolution to Encoder3 improves 0.9 PA-MPJPE.
The results suggest that the lower layers focus on the global interactions of the mesh vertices to model the posture of the human body, while the upper layers pay more attention to the local interactions for better shape reconstruction.
Analysis of Encoder Architecture
We investigate the relationship between the MHSA module (Multi-Head Self-Attention) and the Graph Convolution module by using three different designs:
(i) We use a graph convolution layer and MHSA in parallel, similar to [40]. (ii) We first use a graph convolution layer and then MHSA. (iii) We first use MHSA and then a graph convolution layer.

Effectiveness of Adding Graph Residual Block
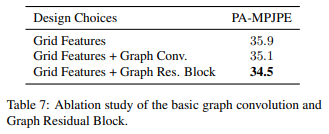
Relationship between Grid Features and Graph Convolution

It shows that grid features and graph convolutions mutually reinforce each other, which leads to an further increase in performance.
Visualization of Local Interactions

Graphormer is able to model both global and local interactions, especially those between the left knee and the left toes. As a result, Graphormer reconstructs a more favorable shape compared to prior works.
6. Conclusion
Graphormer is able to model both global and local interactions, especially those between the left knee and the left toes. As a result, Graphormer reconstructs a more favorable shape compared to prior works.
We explored various model design options and demonstrated that both graph convolutions and grid features are helpful for improving the performance of the transformer.
We explored various model design options and demonstrated that both graph convolutions and grid features are helpful for improving the performance of the transformer.
- 학부생 때 만든 것이라 오류가 있거나, 설명이 부족할 수 있습니다.
Uploaded by N2T
'Paper Summary' 카테고리의 다른 글
| Graph Attention Networks, ICLR’18 (0) | 2023.03.26 |
|---|---|
| GaAN: Gated Attention Networks for Learning on Large and Spatiotemporal Graphs, UAI’18 (0) | 2023.03.26 |
| Learning Actor Relation Graphs for Group Activity Recognition, CVPR’19 (0) | 2023.03.26 |
| Actor-Transformers for Group Activity Recognition, CVPR’20 (0) | 2023.03.26 |
| End-to-end Recovery of Human Shape and Pose, CVPR’18 (0) | 2023.03.26 |
